01. Detect HFOs in Simulated Dataset

MNE-HFO currently depends on the data structures defined by MNE-Python. Namely the mne.io.Raw object.

In this example, we use MNE-HFO to simulate raw data and detect HFOs. Specifically, we will follow these steps:

1. Create some simulated data and artificially simulate a few HFOs

2. Run a few mne_hfo.base.Detector instances to detect HFOs

3. Format the detected HFOs as a pandas.DataFrame

4. Write to disk and read it in again.

# Authors: Adam Li <adam2392@gmail.com>
#

We are importing everything we need for this example:

import numpy as np
from mne import create_info
from mne.io import RawArray

from mne_hfo import (RMSDetector, compute_chs_hfo_rates,
                     events_to_annotations)
from mne_hfo.simulate import simulate_hfo

Simulate the data

First, we need some data to work with. We will use a fake dataset that we simulate.

In this example, we will simulate sinusoidal data that has an artificial HFO added at two points with 9 cycles each.

# simulate the testing dataset
freqs = [2.5, 6.0, 10.0, 16.0, 32.5, 67.5, 165.0,
         250.0, 425.0, 500.0, 800.0, 1500.0]

# sampling frequency
sfreq = 2000

# number of seconds to simulate
n = sfreq * 10
data = np.zeros(n)

# generate some sinusoidal data at specified frequencies
x = np.arange(n)
for freq in freqs:
    # freq_amp = basic_amp / freq
    y = np.sin(2 * np.pi * freq * x / sfreq)
    data += y

# We have dummy data now inject 2 HFOs
freq = 250
numcycles = 9
sim = simulate_hfo(sfreq, freq, numcycles)[0]
ev_start = sfreq
data[ev_start: ev_start + len(sim)] += sim * 10

sim = simulate_hfo(sfreq, freq, numcycles)[0]
ev_start = 7 * sfreq
data[ev_start: ev_start + len(sim)] += sim * 10

# convert the data into mne-python
# note: the channel names are made up and the channel types are just
# set to 'seeg' for the sake of the example
ch_names = ['A1']
info = create_info(sfreq=sfreq, ch_names=ch_names, ch_types='seeg')
raw = RawArray(data=data[np.newaxis, :], info=info)

Out:

Creating RawArray with float64 data, n_channels=1, n_times=20000
    Range : 0 ... 19999 =      0.000 ...     9.999 secs
Ready.

Let’s plot the data and see what it looks like

raw.plot()

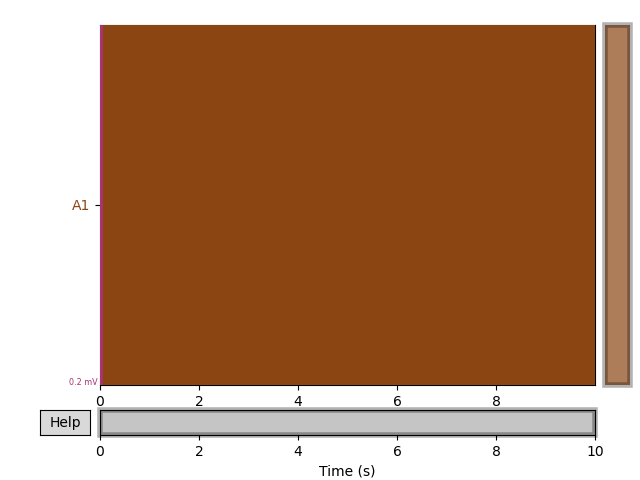
Out:

<MNEBrowseFigure size 640x480 with 4 Axes>

Detect HFOs

All detectors inherit from the base class mne_hfo.base.Detector, which inherits from the sklearn.base.BaseEstimator class. To run any estimator, one instantiates it along with the hyper-parameters, and then calls the fit function. Afterwards, detected HFOs are available in the various data structures. The recommended usage is the DataFrame, which is accessible via the mne_hfo.base.Detector.hfo_df property.

kwargs = {
    'threshold': 3,  # threshold for "significance"
    'win_size': 100,  # window size in samples
    'overlap': 0.25  # overlap in percentage relative to the window size
}
detector = RMSDetector(**kwargs)

# run detector
detector.fit(X=raw)

# get the event dataframe
event_df = detector.hfo_event_df
print(event_df.head())

Out:

  0%|          | 0/1 [00:00<?, ?it/s]
100%|##########| 1/1 [00:00<00:00, 72.51it/s]
   onset  duration  sample trial_type
0    1.0     0.075    2000     hfo_A1
1    7.0     0.075   14000     hfo_A1

Convert HFO events to annotations

Detectors output HFO events detected as a DataFrame fashioned after the *_events.tsv files in BIDS-iEEG. Instead, HFO events are indeed Derivatives of the Raw data, that are estimated/detected using mne-hfo. The correct way to store them is in terms of an *_annotations.tsv, according to the BIDS-Derivatives specification.

# convert event df -> annotation df
annot_df = events_to_annotations(event_df)
print(annot_df.head())

Out:

   onset  duration label channels   sample
0    1.0     0.075   hfo       A1   2000.0
1    7.0     0.075   hfo       A1  14000.0

compute HFO rate as HFOs per second

ch_rates = compute_chs_hfo_rates(annot_df=annot_df, rate='s')
print(ch_rates)

Out:

Beginning timestamp: 2021-06-07 18:39:26.110282+00:00
Got end timestamp of: 2021-06-07 18:39:33.110282+00:00
Found HFO rate per s for A1 as 0.2857142857142857
defaultdict(<class 'list'>, {'A1': 0.2857142857142857})

Using MNE-HFO 02. Detect HFOs on BIDS Dataset