Note
Click here to download the full example code
Compute source power estimate by projecting the covariance with MNE¶
We can apply the MNE inverse operator to a covariance matrix to obtain an estimate of source power. This is computationally more efficient than first estimating the source timecourses and then computing their power.
# Author: Denis A. Engemann <denis-alexander.engemann@inria.fr>
# Luke Bloy <luke.bloy@gmail.com>
#
# License: BSD (3-clause)
import os.path as op
import numpy as np
import mne
from mne.datasets import sample
from mne.minimum_norm import make_inverse_operator, apply_inverse_cov
data_path = sample.data_path()
subjects_dir = data_path + '/subjects'
raw_fname = data_path + '/MEG/sample/sample_audvis_filt-0-40_raw.fif'
raw = mne.io.read_raw_fif(raw_fname)
Out:
Opening raw data file /home/circleci/mne_data/MNE-sample-data/MEG/sample/sample_audvis_filt-0-40_raw.fif...
Read a total of 4 projection items:
PCA-v1 (1 x 102) idle
PCA-v2 (1 x 102) idle
PCA-v3 (1 x 102) idle
Average EEG reference (1 x 60) idle
Range : 6450 ... 48149 = 42.956 ... 320.665 secs
Ready.
Compute empty-room covariance¶
First we compute an empty-room covariance, which captures noise from the sensors and environment.
raw_empty_room_fname = op.join(
data_path, 'MEG', 'sample', 'ernoise_raw.fif')
raw_empty_room = mne.io.read_raw_fif(raw_empty_room_fname)
raw_empty_room.crop(0, 60)
raw_empty_room.info['bads'] = ['MEG 2443']
raw_empty_room.info['projs'] = raw.info['projs']
noise_cov = mne.compute_raw_covariance(
raw_empty_room, method=['empirical', 'shrunk'])
del raw_empty_room
Out:
Opening raw data file /home/circleci/mne_data/MNE-sample-data/MEG/sample/ernoise_raw.fif...
Isotrak not found
Read a total of 3 projection items:
PCA-v1 (1 x 102) idle
PCA-v2 (1 x 102) idle
PCA-v3 (1 x 102) idle
Range : 19800 ... 85867 = 32.966 ... 142.965 secs
Ready.
Using up to 300 segments
Computing rank from data with rank=None
Using tolerance 3e-09 (2.2e-16 eps * 305 dim * 4.4e+04 max singular value)
Estimated rank (mag + grad): 302
MEG: rank 302 computed from 305 data channels with 3 projectors
Created an SSP operator (subspace dimension = 3)
Setting small MEG eigenvalues to zero (without PCA)
Reducing data rank from 305 -> 302
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using SHRUNK
Done.
Using cross-validation to select the best estimator.
Number of samples used : 36000
log-likelihood on unseen data (descending order):
shrunk: -1588.456
empirical: -1589.805
selecting best estimator: shrunk
[done]
Epoch the data¶
raw.info['bads'] = ['MEG 2443', 'EEG 053']
raw.load_data().filter(4, 12)
events = mne.find_events(raw, stim_channel='STI 014')
event_id = dict(aud_l=1, aud_r=2, vis_l=3, vis_r=4)
tmin, tmax = -0.2, 0.5
baseline = (None, 0) # means from the first instant to t = 0
reject = dict(grad=4000e-13, mag=4e-12, eog=150e-6)
epochs = mne.Epochs(raw.copy().filter(4, 12), events, event_id, tmin, tmax,
proj=True, picks=('meg', 'eog'), baseline=None,
reject=reject, preload=True)
del raw
Out:
Reading 0 ... 41699 = 0.000 ... 277.709 secs...
Filtering raw data in 1 contiguous segment
Setting up band-pass filter from 4 - 12 Hz
FIR filter parameters
---------------------
Designing a one-pass, zero-phase, non-causal bandpass filter:
- Windowed time-domain design (firwin) method
- Hamming window with 0.0194 passband ripple and 53 dB stopband attenuation
- Lower passband edge: 4.00
- Lower transition bandwidth: 2.00 Hz (-6 dB cutoff frequency: 3.00 Hz)
- Upper passband edge: 12.00 Hz
- Upper transition bandwidth: 3.00 Hz (-6 dB cutoff frequency: 13.50 Hz)
- Filter length: 249 samples (1.658 sec)
319 events found
Event IDs: [ 1 2 3 4 5 32]
Filtering raw data in 1 contiguous segment
Setting up band-pass filter from 4 - 12 Hz
FIR filter parameters
---------------------
Designing a one-pass, zero-phase, non-causal bandpass filter:
- Windowed time-domain design (firwin) method
- Hamming window with 0.0194 passband ripple and 53 dB stopband attenuation
- Lower passband edge: 4.00
- Lower transition bandwidth: 2.00 Hz (-6 dB cutoff frequency: 3.00 Hz)
- Upper passband edge: 12.00 Hz
- Upper transition bandwidth: 3.00 Hz (-6 dB cutoff frequency: 13.50 Hz)
- Filter length: 249 samples (1.658 sec)
Not setting metadata
Not setting metadata
288 matching events found
No baseline correction applied
Created an SSP operator (subspace dimension = 3)
4 projection items activated
Loading data for 288 events and 106 original time points ...
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on MAG : ['MEG 1711']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
Rejecting epoch based on EOG : ['EOG 061']
48 bad epochs dropped
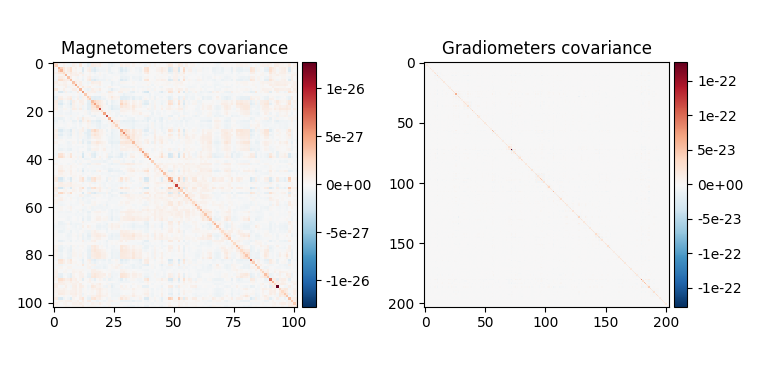
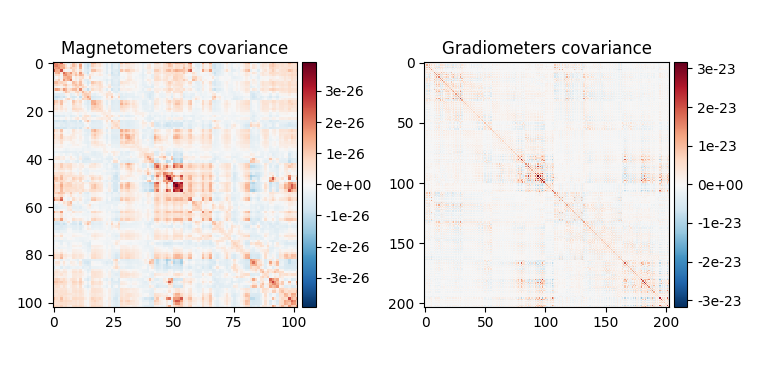
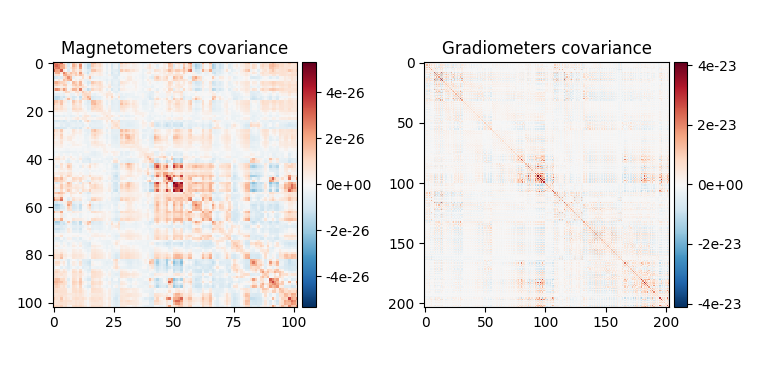
Compute and plot covariances¶
In addition to the empty-room covariance above, we compute two additional covariances:
Baseline covariance, which captures signals not of interest in our analysis (e.g., sensor noise, environmental noise, physiological artifacts, and also resting-state-like brain activity / “noise”).
Data covariance, which captures our activation of interest (in addition to noise sources).
base_cov = mne.compute_covariance(
epochs, tmin=-0.2, tmax=0, method=['shrunk', 'empirical'], rank=None,
verbose=True)
data_cov = mne.compute_covariance(
epochs, tmin=0., tmax=0.2, method=['shrunk', 'empirical'], rank=None,
verbose=True)
fig_noise_cov = mne.viz.plot_cov(noise_cov, epochs.info, show_svd=False)
fig_base_cov = mne.viz.plot_cov(base_cov, epochs.info, show_svd=False)
fig_data_cov = mne.viz.plot_cov(data_cov, epochs.info, show_svd=False)
Out:
Computing rank from data with rank=None
Using tolerance 3.9e-09 (2.2e-16 eps * 305 dim * 5.8e+04 max singular value)
Estimated rank (mag + grad): 302
MEG: rank 302 computed from 305 data channels with 3 projectors
Created an SSP operator (subspace dimension = 3)
Setting small MEG eigenvalues to zero (without PCA)
Reducing data rank from 305 -> 302
Estimating covariance using SHRUNK
Done.
Estimating covariance using EMPIRICAL
Done.
Using cross-validation to select the best estimator.
Number of samples used : 7440
log-likelihood on unseen data (descending order):
shrunk: -1308.077
empirical: -1344.171
selecting best estimator: shrunk
[done]
Computing rank from data with rank=None
Using tolerance 4.4e-09 (2.2e-16 eps * 305 dim * 6.5e+04 max singular value)
Estimated rank (mag + grad): 302
MEG: rank 302 computed from 305 data channels with 3 projectors
Created an SSP operator (subspace dimension = 3)
Setting small MEG eigenvalues to zero (without PCA)
Reducing data rank from 305 -> 302
Estimating covariance using SHRUNK
Done.
Estimating covariance using EMPIRICAL
Done.
Using cross-validation to select the best estimator.
Number of samples used : 7440
log-likelihood on unseen data (descending order):
shrunk: -1314.135
empirical: -1350.783
selecting best estimator: shrunk
[done]
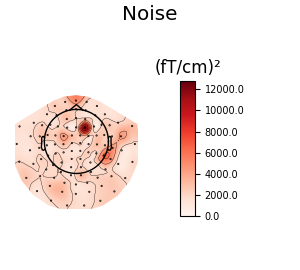
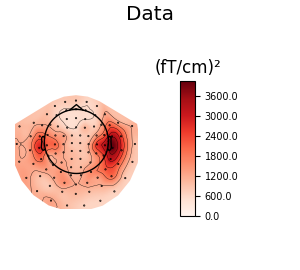
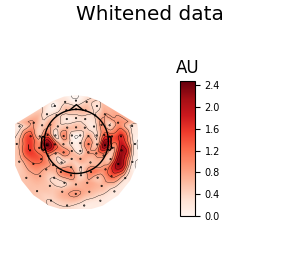
We can also look at the covariances using topomaps, here we just show the baseline and data covariances, followed by the data covariance whitened by the baseline covariance:
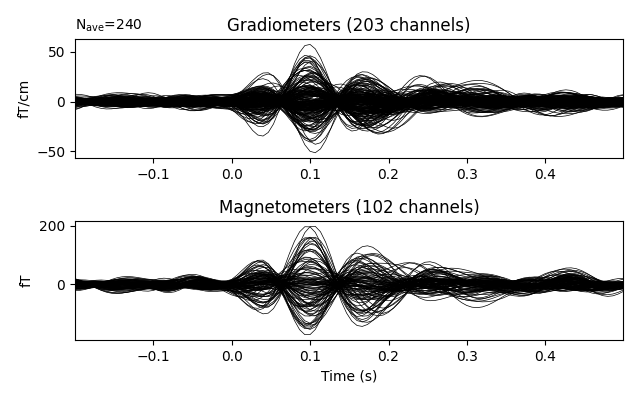
evoked = epochs.average().pick('meg')
evoked.drop_channels(evoked.info['bads'])
evoked.plot(time_unit='s')
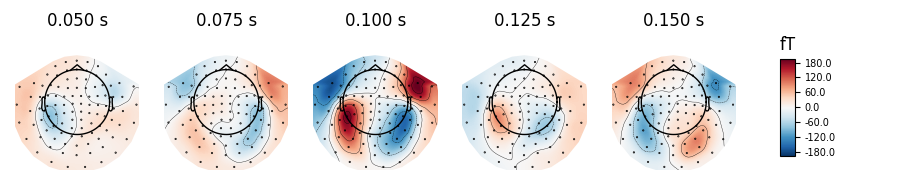
evoked.plot_topomap(times=np.linspace(0.05, 0.15, 5), ch_type='mag')
noise_cov.plot_topomap(evoked.info, 'grad', title='Noise')
data_cov.plot_topomap(evoked.info, 'grad', title='Data')
data_cov.plot_topomap(evoked.info, 'grad', noise_cov=noise_cov,
title='Whitened data')
Out:
Removing projector <Projection | Average EEG reference, active : True, n_channels : 60>
Removing projector <Projection | PCA-v1, active : True, n_channels : 102>
Removing projector <Projection | PCA-v2, active : True, n_channels : 102>
Removing projector <Projection | PCA-v3, active : True, n_channels : 102>
Removing projector <Projection | PCA-v1, active : True, n_channels : 102>
Removing projector <Projection | PCA-v2, active : True, n_channels : 102>
Removing projector <Projection | PCA-v3, active : True, n_channels : 102>
Created an SSP operator (subspace dimension = 3)
Computing rank from covariance with rank=None
Using tolerance 1.4e-13 (2.2e-16 eps * 305 dim * 2 max singular value)
Estimated rank (mag + grad): 302
MEG: rank 302 computed from 305 data channels with 3 projectors
Setting small MEG eigenvalues to zero (without PCA)
Created the whitener using a noise covariance matrix with rank 302 (3 small eigenvalues omitted)
Created an SSP operator (subspace dimension = 3)
Computing rank from covariance with rank=None
Using tolerance 1.4e-13 (2.2e-16 eps * 305 dim * 2 max singular value)
Estimated rank (mag + grad): 302
MEG: rank 302 computed from 305 data channels with 3 projectors
Setting small MEG eigenvalues to zero (without PCA)
Created the whitener using a noise covariance matrix with rank 302 (3 small eigenvalues omitted)
Removing projector <Projection | PCA-v1, active : True, n_channels : 102>
Removing projector <Projection | PCA-v2, active : True, n_channels : 102>
Removing projector <Projection | PCA-v3, active : True, n_channels : 102>
Apply inverse operator to covariance¶
Finally, we can construct an inverse using the empty-room noise covariance:
# Read the forward solution and compute the inverse operator
fname_fwd = data_path + '/MEG/sample/sample_audvis-meg-oct-6-fwd.fif'
fwd = mne.read_forward_solution(fname_fwd)
# make an MEG inverse operator
info = evoked.info
inverse_operator = make_inverse_operator(info, fwd, noise_cov,
loose=0.2, depth=0.8)
Out:
Reading forward solution from /home/circleci/mne_data/MNE-sample-data/MEG/sample/sample_audvis-meg-oct-6-fwd.fif...
Reading a source space...
Computing patch statistics...
Patch information added...
Distance information added...
[done]
Reading a source space...
Computing patch statistics...
Patch information added...
Distance information added...
[done]
2 source spaces read
Desired named matrix (kind = 3523) not available
Read MEG forward solution (7498 sources, 306 channels, free orientations)
Source spaces transformed to the forward solution coordinate frame
Converting forward solution to surface orientation
Average patch normals will be employed in the rotation to the local surface coordinates....
Converting to surface-based source orientations...
[done]
Computing inverse operator with 305 channels.
305 out of 306 channels remain after picking
Selected 305 channels
Creating the depth weighting matrix...
203 planar channels
limit = 7265/7498 = 10.037795
scale = 2.52065e-08 exp = 0.8
Applying loose dipole orientations to surface source spaces: 0.2
Whitening the forward solution.
Created an SSP operator (subspace dimension = 3)
Computing rank from covariance with rank=None
Using tolerance 1.4e-13 (2.2e-16 eps * 305 dim * 2 max singular value)
Estimated rank (mag + grad): 302
MEG: rank 302 computed from 305 data channels with 3 projectors
Setting small MEG eigenvalues to zero (without PCA)
Creating the source covariance matrix
Adjusting source covariance matrix.
Computing SVD of whitened and weighted lead field matrix.
largest singular value = 6.38809
scaling factor to adjust the trace = 5.27749e+19
Project our data and baseline covariance to source space:
stc_data = apply_inverse_cov(data_cov, evoked.info, inverse_operator,
nave=len(epochs), method='dSPM', verbose=True)
stc_base = apply_inverse_cov(base_cov, evoked.info, inverse_operator,
nave=len(epochs), method='dSPM', verbose=True)
Out:
Preparing the inverse operator for use...
Scaled noise and source covariance from nave = 1 to nave = 240
Created the regularized inverter
Created an SSP operator (subspace dimension = 3)
Created the whitener using a noise covariance matrix with rank 302 (3 small eigenvalues omitted)
Computing noise-normalization factors (dSPM)...
[done]
Applying inverse operator to "cov"...
Picked 305 channels from the data
Computing inverse...
Eigenleads need to be weighted ...
Computing residual...
Explained 37.2% variance
dSPM...
Combining the current components...
[done]
Preparing the inverse operator for use...
Scaled noise and source covariance from nave = 1 to nave = 240
Created the regularized inverter
Created an SSP operator (subspace dimension = 3)
Created the whitener using a noise covariance matrix with rank 302 (3 small eigenvalues omitted)
Computing noise-normalization factors (dSPM)...
[done]
Applying inverse operator to "cov"...
Picked 305 channels from the data
Computing inverse...
Eigenleads need to be weighted ...
Computing residual...
Explained 37.2% variance
dSPM...
Combining the current components...
[done]
And visualize power is relative to the baseline:
stc_data /= stc_base
brain = stc_data.plot(subject='sample', subjects_dir=subjects_dir,
clim=dict(kind='percent', lims=(50, 90, 98)))
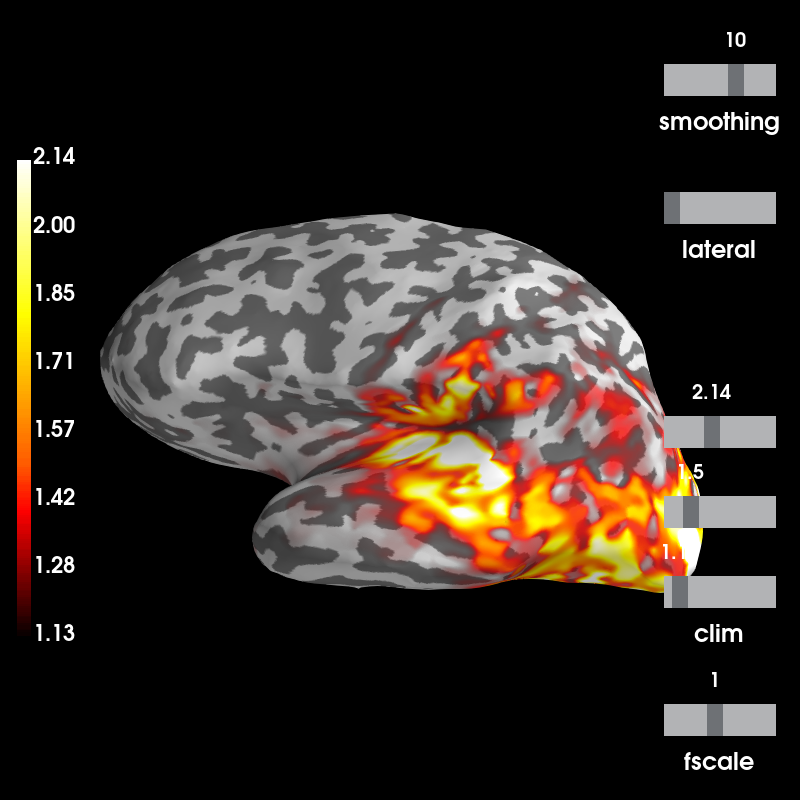
Out:
Using control points [1.13405797 1.49777712 2.14096143]
Total running time of the script: ( 0 minutes 31.410 seconds)
Estimated memory usage: 398 MB