mne.Covariance¶

class mne.Covariance(data, names, bads, projs, nfree, eig=None, eigvec=None, method=None, loglik=None, verbose=None)[source]¶

Noise covariance matrix.

Warning

This class should not be instantiated directly, but instead should be created using a covariance reading or computation function.

Parameters

dataarray_like: The data.
nameslist of str: Channel names.
badslist of str: Bad channels.
projslist: Projection vectors.
nfreeint: Degrees of freedom.
eigarray_like | None: Eigenvalues.
eigvecarray_like | None: Eigenvectors.
methodstr | None: The method used to compute the covariance.
loglikfloat: The log likelihood.
verbosebool, str, int, or None: If not None, override default verbose level (see mne.verbose() and Logging documentation for more). If used, it should be passed as a keyword-argument only. Defaults to self.verbose.

See also

compute_covariance
compute_raw_covariance
make_ad_hoc_cov
read_cov

Attributes

dataarray of shape (n_channels, n_channels): Numpy array of Noise covariance matrix.
ch_nameslist of str: Channel names.
nfreeint: Number of degrees of freedom.
dimint: The number of channels n_channels.

Methods

`__add__`(cov)	Add Covariance taking into account number of degrees of freedom.
`__contains__`(key, /)	True if the dictionary has the specified key, else False.
`__getitem__`	x.__getitem__(y) <==> x[y]
`__iter__`(/)	Implement iter(self).
`__len__`(/)	Return len(self).
`as_diag`()	Set covariance to be processed as being diagonal.
`clear`()
`copy`()	Copy the Covariance object.
`fromkeys`(iterable[, value])	Create a new dictionary with keys from iterable and values set to value.
`get`(key[, default])	Return the value for key if key is in the dictionary, else default.
`items`()
`keys`()
`pick_channels`(ch_names[, ordered])	Pick channels from this covariance matrix.
`plot`(info[, exclude, colorbar, proj, …])	Plot Covariance data.
`plot_topomap`(info[, ch_type, vmin, vmax, …])	Plot a topomap of the covariance diagonal.
`pop`(k[,d])	If key is not found, d is returned if given, otherwise KeyError is raised
`popitem`(/)	Remove and return a (key, value) pair as a 2-tuple.
`save`(fname)	Save covariance matrix in a FIF file.
`setdefault`(key[, default])	Insert key with a value of default if key is not in the dictionary.
`update`([E, ]**F)	If E is present and has a .keys() method, then does: for k in E: D[k] = E[k] If E is present and lacks a .keys() method, then does: for k, v in E: D[k] = v In either case, this is followed by: for k in F: D[k] = F[k]
`values`()

__add__(cov)[source]¶: Add Covariance taking into account number of degrees of freedom.

__contains__(key, /)¶: True if the dictionary has the specified key, else False.

__getitem__()¶: x.__getitem__(y) <==> x[y]

__iter__(/)¶: Implement iter(self).

__len__(/)¶: Return len(self).

as_diag()[source]¶

Set covariance to be processed as being diagonal.

Returns

covdict: The covariance.

Notes

This function allows creation of inverse operators equivalent to using the old “–diagnoise” mne option.

This function operates in place.

property ch_names¶: Channel names.

clear() → None. Remove all items from D.¶

copy()[source]¶

Copy the Covariance object.

Returns

covinstance of Covariance: The copied object.

property data¶: Numpy array of Noise covariance matrix.

fromkeys(iterable, value=None, /)¶: Create a new dictionary with keys from iterable and values set to value.

get(key, default=None, /)¶: Return the value for key if key is in the dictionary, else default.

items() → a set-like object providing a view on D’s items¶

keys() → a set-like object providing a view on D’s keys¶

property nfree¶: Number of degrees of freedom.

pick_channels(ch_names, ordered=False)[source]¶

Pick channels from this covariance matrix.

Parameters

ch_nameslist of str: List of channels to keep. All other channels are dropped.
orderedbool: If True (default False), ensure that the order of the channels matches the order of ch_names.

Returns

covinstance of Covariance.: The modified covariance matrix.

Notes

Operates in-place.

New in version 0.20.0.

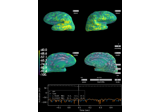
plot(info, exclude=[], colorbar=True, proj=False, show_svd=True, show=True, verbose=None)[source]¶

Plot Covariance data.

Parameters

infodict: Measurement info.
excludelist of str | str: List of channels to exclude. If empty do not exclude any channel. If ‘bads’, exclude info[‘bads’].
colorbarbool: Show colorbar or not.
projbool: Apply projections or not.
show_svdbool: Plot also singular values of the noise covariance for each sensor type. We show square roots ie. standard deviations.
showbool: Show figure if True.
verbosebool, str, int, or None: If not None, override default verbose level (see mne.verbose() and Logging documentation for more). If used, it should be passed as a keyword-argument only.

Returns

fig_covinstance of matplotlib.figure.Figure: The covariance plot.
fig_svdinstance of matplotlib.figure.Figure | None: The SVD spectra plot of the covariance.

See also

mne.compute_rank

Notes

For each channel type, the rank is estimated using mne.compute_rank().

Changed in version 0.19: Approximate ranks for each channel type are shown with red dashed lines.

Examples using plot:

Reading/Writing a noise covariance matrix¶

Source reconstruction using an LCMV beamformer¶

Computing a covariance matrix¶

Brainstorm auditory tutorial dataset¶

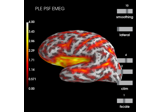
plot_topomap(info, ch_type=None, vmin=None, vmax=None, cmap=None, sensors=True, colorbar=True, scalings=None, units=None, res=64, size=1, cbar_fmt='%3.1f', proj=False, show=True, show_names=False, title=None, mask=None, mask_params=None, outlines='head', contours=6, image_interp='bilinear', axes=None, extrapolate='auto', sphere=None, border='mean', noise_cov=None, verbose=None)[source]¶

Plot a topomap of the covariance diagonal.

Parameters

infoinstance of Info

The measurement information.

ch_typestr

The channel type being plotted. Determines the 'auto' extrapolation mode.

New in version 0.21.

vmin, vmaxfloat | callable() | None

Lower and upper bounds of the colormap, in the same units as the data. If vmin and vmax are both None, they are set at ± the maximum absolute value of the data (yielding a colormap with midpoint at 0). If only one of vmin, vmax is None, will use min(data) or max(data), respectively. If callable, should accept a NumPy array of data and return a float.

cmapmatplotlib colormap | (colormap, bool) | ‘interactive’ | None

Colormap to use. If tuple, the first value indicates the colormap to use and the second value is a boolean defining interactivity. In interactive mode the colors are adjustable by clicking and dragging the colorbar with left and right mouse button. Left mouse button moves the scale up and down and right mouse button adjusts the range (zoom). The mouse scroll can also be used to adjust the range. Hitting space bar resets the range. Up and down arrows can be used to change the colormap. If None (default), ‘Reds’ is used for all positive data, otherwise defaults to ‘RdBu_r’. If ‘interactive’, translates to (None, True).

Warning

Interactive mode works smoothly only for a small amount of topomaps. Interactive mode is disabled by default for more than 2 topomaps.

sensorsbool | str

Add markers for sensor locations to the plot. Accepts matplotlib plot format string (e.g., ‘r+’ for red plusses). If True (default), circles will be used.

colorbarbool

Plot a colorbar in the rightmost column of the figure.

scalingsdict | float | None

The scalings of the channel types to be applied for plotting. If None, defaults to dict(eeg=1e6, grad=1e13, mag=1e15).

unitsdict | str | None

The unit of the channel type used for colorbar label. If scale is None the unit is automatically determined.

resint

The resolution of the topomap image (n pixels along each side).

sizefloat

Side length per topomap in inches.

cbar_fmtstr

String format for colorbar values.

projbool | ‘interactive’ | ‘reconstruct’

If true SSP projections are applied before display. If ‘interactive’, a check box for reversible selection of SSP projection vectors will be shown. If ‘reconstruct’, projection vectors will be applied and then M/EEG data will be reconstructed via field mapping to reduce the signal bias caused by projection.

Changed in version 0.21: Support for ‘reconstruct’ was added.

showbool

Show figure if True.

show_namesbool | callable()

If True, show channel names on top of the map. If a callable is passed, channel names will be formatted using the callable; e.g., to delete the prefix ‘MEG ‘ from all channel names, pass the function lambda x: x.replace('MEG ', ''). If mask is not None, only significant sensors will be shown.

titlestr | None

Title. If None (default), no title is displayed.

maskndarray of bool, shape (n_channels, n_times) | None

The channels to be marked as significant at a given time point. Indices set to True will be considered. Defaults to None.

mask_paramsdict | None

Additional plotting parameters for plotting significant sensors. Default (None) equals:

dict(marker='o', markerfacecolor='w', markeredgecolor='k',
        linewidth=0, markersize=4)

outlines‘head’ | ‘skirt’ | dict | None

The outlines to be drawn. If ‘head’, the default head scheme will be drawn. If ‘skirt’ the head scheme will be drawn, but sensors are allowed to be plotted outside of the head circle. If dict, each key refers to a tuple of x and y positions, the values in ‘mask_pos’ will serve as image mask. Alternatively, a matplotlib patch object can be passed for advanced masking options, either directly or as a function that returns patches (required for multi-axis plots). If None, nothing will be drawn. Defaults to ‘head’.

contoursint | array of float

The number of contour lines to draw. If 0, no contours will be drawn. When an integer, matplotlib ticker locator is used to find suitable values for the contour thresholds (may sometimes be inaccurate, use array for accuracy). If an array, the values represent the levels for the contours. The values are in µV for EEG, fT for magnetometers and fT/m for gradiometers. If colorbar=True, the ticks in colorbar correspond to the contour levels. Defaults to 6.

image_interpstr

The image interpolation to be used. All matplotlib options are accepted.

axesinstance of Axes | list | None

The axes to plot to. If list, the list must be a list of Axes of the same length as times (unless times is None). If instance of Axes, times must be a float or a list of one float. Defaults to None.

extrapolatestr

Options:

'box'
Extrapolate to four points placed to form a square encompassing all data points, where each side of the square is three times the range of the data in the respective dimension.
'local' (default)
Extrapolate only to nearby points (approximately to points closer than median inter-electrode distance). This will also set the mask to be polygonal based on the convex hull of the sensors.
'head'
Extrapolate out to the edges of the clipping circle. This will be on the head circle when the sensors are contained within the head circle, but it can extend beyond the head when sensors are plotted outside the head circle.

Changed in version 0.21:

The default was changed to 'local'
'local' was changed to use a convex hull mask
'head' was changed to extrapolate out to the clipping circle.

spherefloat | array_like | str | None

The sphere parameters to use for the cartoon head. Can be array-like of shape (4,) to give the X/Y/Z origin and radius in meters, or a single float to give the radius (origin assumed 0, 0, 0). Can also be a spherical ConductorModel, which will use the origin and radius. Can be “auto” to use a digitization-based fit. Can also be None (default) to use ‘auto’ when enough extra digitization points are available, and 0.095 otherwise. Currently the head radius does not affect plotting.

New in version 0.20.

borderfloat | ‘mean’

Value to extrapolate to on the topomap borders. If 'mean' (default), then each extrapolated point has the average value of its neighbours.

New in version 0.20.

noise_covinstance of Covariance | None

If not None, whiten the instance with noise_cov before plotting.

verbosebool, str, int, or None

If not None, override default verbose level (see mne.verbose() and Logging documentation for more). If used, it should be passed as a keyword-argument only.

Returns

figinstance of Figure: The matplotlib figure.

Notes

New in version 0.21.

Examples using plot_topomap:

Compute source power estimate by projecting the covariance with MNE¶

pop(k[, d]) → v, remove specified key and return the corresponding value.¶: If key is not found, d is returned if given, otherwise KeyError is raised

popitem(/)¶

Remove and return a (key, value) pair as a 2-tuple.

Pairs are returned in LIFO (last-in, first-out) order. Raises KeyError if the dict is empty.

save(fname)[source]¶

Save covariance matrix in a FIF file.

Parameters

fnamestr: Output filename.

setdefault(key, default=None, /)¶

Insert key with a value of default if key is not in the dictionary.

Return the value for key if key is in the dictionary, else default.

update([E, ]**F) → None. Update D from dict/iterable E and F.¶: If E is present and has a .keys() method, then does: for k in E: D[k] = E[k] If E is present and lacks a .keys() method, then does: for k, v in E: D[k] = v In either case, this is followed by: for k in F: D[k] = F[k]