mne.minimum_norm.InverseOperator#
- class mne.minimum_norm.InverseOperator[source]#
InverseOperator class to represent info from inverse operator.
- Attributes:
Methods
__contains__(key, /)True if the dictionary has the specified key, else False.
x.__getitem__(y) <==> x[y]
__iter__(/)Implement iter(self).
__len__(/)Return len(self).
clear()copy()Return a copy of the InverseOperator.
fromkeys(iterable[, value])Create a new dictionary with keys from iterable and values set to value.
get(key[, default])Return the value for key if key is in the dictionary, else default.
items()keys()pop(key[, default])If the key is not found, return the default if given; otherwise, raise a KeyError.
popitem(/)Remove and return a (key, value) pair as a 2-tuple.
setdefault(key[, default])Insert key with a value of default if key is not in the dictionary.
update([E, ]**F)If E is present and has a .keys() method, then does: for k in E: D[k] = E[k] If E is present and lacks a .keys() method, then does: for k, v in E: D[k] = v In either case, this is followed by: for k in F: D[k] = F[k]
values()- __contains__(key, /)#
True if the dictionary has the specified key, else False.
- __getitem__()#
x.__getitem__(y) <==> x[y]
- __iter__(/)#
Implement iter(self).
- __len__(/)#
Return len(self).
- property ch_names#
Name of channels attached to the inverse operator.
- clear() None. Remove all items from D.#
- fromkeys(iterable, value=None, /)#
Create a new dictionary with keys from iterable and values set to value.
- get(key, default=None, /)#
Return the value for key if key is in the dictionary, else default.
- items() a set-like object providing a view on D's items#
- keys() a set-like object providing a view on D's keys#
- pop(key, default=<unrepresentable>, /)#
If the key is not found, return the default if given; otherwise, raise a KeyError.
- popitem(/)#
Remove and return a (key, value) pair as a 2-tuple.
Pairs are returned in LIFO (last-in, first-out) order. Raises KeyError if the dict is empty.
- setdefault(key, default=None, /)#
Insert key with a value of default if key is not in the dictionary.
Return the value for key if key is in the dictionary, else default.
- update([E, ]**F) None. Update D from dict/iterable E and F.#
If E is present and has a .keys() method, then does: for k in E: D[k] = E[k] If E is present and lacks a .keys() method, then does: for k, v in E: D[k] = v In either case, this is followed by: for k in F: D[k] = F[k]
- values() an object providing a view on D's values#
Examples using mne.minimum_norm.InverseOperator#
Working with CTF data: the Brainstorm auditory dataset
Preprocessing optically pumped magnetometer (OPM) MEG data
Source localization with MNE, dSPM, sLORETA, and eLORETA
The role of dipole orientations in distributed source localization
EEG source localization given electrode locations on an MRI
Permutation t-test on source data with spatio-temporal clustering
Repeated measures ANOVA on source data with spatio-temporal clustering
Compute Power Spectral Density of inverse solution from single epochs

Compute power and phase lock in label of the source space
Compute source power spectral density (PSD) in a label

Compute induced power in the source space with dSPM

Compute MNE-dSPM inverse solution on single epochs
Compute MNE-dSPM inverse solution on evoked data in volume source space
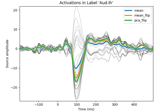
Extracting the time series of activations in a label
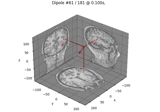
Compute sparse inverse solution with mixed norm: MxNE and irMxNE
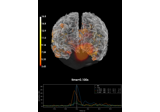
Compute MNE inverse solution on evoked data with a mixed source space
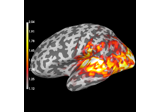
Compute source power estimate by projecting the covariance with MNE

Computing source timecourses with an XFit-like multi-dipole model
Plot point-spread functions (PSFs) and cross-talk functions (CTFs)
Compute spatial resolution metrics in source space
Compute spatial resolution metrics to compare MEG with EEG+MEG