Note
Go to the end to download the full example code.
Source-level RSA using a searchlight on surface data#
This example demonstrates how to perform representational similarity analysis (RSA) on source localized MEG data, using a searchlight approach.
In the searchlight approach, representational similarity is computed between the model and searchlight “patches”. A patch is defined by a seed vertex on the cortex and all vertices within a given radius. By default, patches are created using each vertex as a seed point, so you can think of it as a “searchlight” that scans along the cortex.
The radius of a searchlight can be defined in space, in time, or both. In this example, our searchlight will have a spatial radius of 2 cm. and a temporal radius of 20 ms.
The dataset will be the MNE-sample dataset: a collection of 288 epochs in which the participant was presented with an auditory beep or visual stimulus to either the left or right ear or visual field.
# sphinx_gallery_thumbnail_number=2
import mne
import mne_rsa
# Import required packages
from matplotlib import pyplot as plt
mne.set_log_level(False) # Be less verbose
mne.viz.set_3d_backend("pyvista")
'pyvistaqt'
We’ll be using the data from the MNE-sample set. To speed up computations in this example, we’re going to use one of the sparse source spaces from the testing set.
sample_root = mne.datasets.sample.data_path(verbose=True)
testing_root = mne.datasets.testing.data_path(verbose=True)
sample_path = sample_root / "MEG" / "sample"
testing_path = testing_root / "MEG" / "sample"
subjects_dir = sample_root / "subjects"
Creating epochs from the continuous (raw) data. We downsample to 100 Hz to speed up the RSA computations later on.
raw = mne.io.read_raw_fif(sample_path / "sample_audvis_filt-0-40_raw.fif")
events = mne.read_events(sample_path / "sample_audvis_filt-0-40_raw-eve.fif")
event_id = {"audio/left": 1, "audio/right": 2, "visual/left": 3, "visual/right": 4}
epochs = mne.Epochs(raw, events, event_id, preload=True)
epochs.resample(100)
It’s important that the model RDM and the epochs are in the same order, so that each row in the model RDM will correspond to an epoch. The model RDM will be easier to interpret visually if the data is ordered such that all epochs belonging to the same experimental condition are right next to each-other, so patterns jump out. This can be achieved by first splitting the epochs by experimental condition and then concatenating them together again.
epoch_splits = [
epochs[cl] for cl in ["audio/left", "audio/right", "visual/left", "visual/right"]
]
epochs = mne.concatenate_epochs(epoch_splits)
Now that the epochs are in the proper order, we can create a RDM based on the experimental conditions. This type of RDM is referred to as a “sensitivity RDM”. Let’s create a sensitivity RDM that will pick up the left auditory response when RSA-ed against the MEG data. Since we want to capture areas where left beeps generate a large signal, we specify that left beeps should be similar to other left beeps. Since we do not want areas where visual stimuli generate a large signal, we specify that beeps must be different from visual stimuli. Furthermore, since in areas where visual stimuli generate only a small signal, random noise will dominate, we also specify that visual stimuli are different from other visual stimuli. Finally left and right auditory beeps will be somewhat similar.
def sensitivity_metric(event_id_1, event_id_2):
"""Determine similarity between two epochs, given their event ids."""
if event_id_1 == 1 and event_id_2 == 1:
return 0 # Completely similar
if event_id_1 == 2 and event_id_2 == 2:
return 0.5 # Somewhat similar
elif event_id_1 == 1 and event_id_2 == 2:
return 0.5 # Somewhat similar
elif event_id_1 == 2 and event_id_1 == 1:
return 0.5 # Somewhat similar
else:
return 1 # Not similar at all
model_rdm = mne_rsa.compute_rdm(epochs.events[:, 2], metric=sensitivity_metric)
mne_rsa.plot_rdms(model_rdm, title="Model RDM")
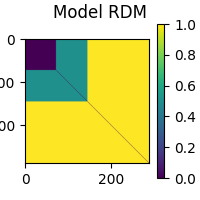
<Figure size 200x200 with 2 Axes>
This example is going to be on source-level, so let’s load the inverse operator and apply it to obtain a cortical surface source estimate for each epoch. To speed up the computation, we going to load an inverse operator from the testing dataset that was created using a sparse source space with not too many vertices.
inv = mne.minimum_norm.read_inverse_operator(
testing_path / "sample_audvis_trunc-meg-eeg-oct-4-meg-inv.fif"
)
epochs_stc = mne.minimum_norm.apply_inverse_epochs(epochs, inv, lambda2=0.1111)
Performing the RSA. This will take some time. Consider increasing n_jobs to
parallelize the computation across multiple CPUs.
rsa_vals = mne_rsa.rsa_stcs(
epochs_stc, # The source localized epochs
model_rdm, # The model RDM we constructed above
src=inv["src"], # The inverse operator has our source space
stc_rdm_metric="correlation", # Metric to compute the MEG RDMs
rsa_metric="kendall-tau-a", # Metric to compare model and EEG RDMs
spatial_radius=0.02, # Spatial radius of the searchlight patch
temporal_radius=0.02, # Temporal radius of the searchlight path
tmin=0,
tmax=0.3, # To save time, only analyze this time interval
n_jobs=1, # Only use one CPU core. Increase this for more speed.
verbose=True,
) # Set to True to display a progress bar
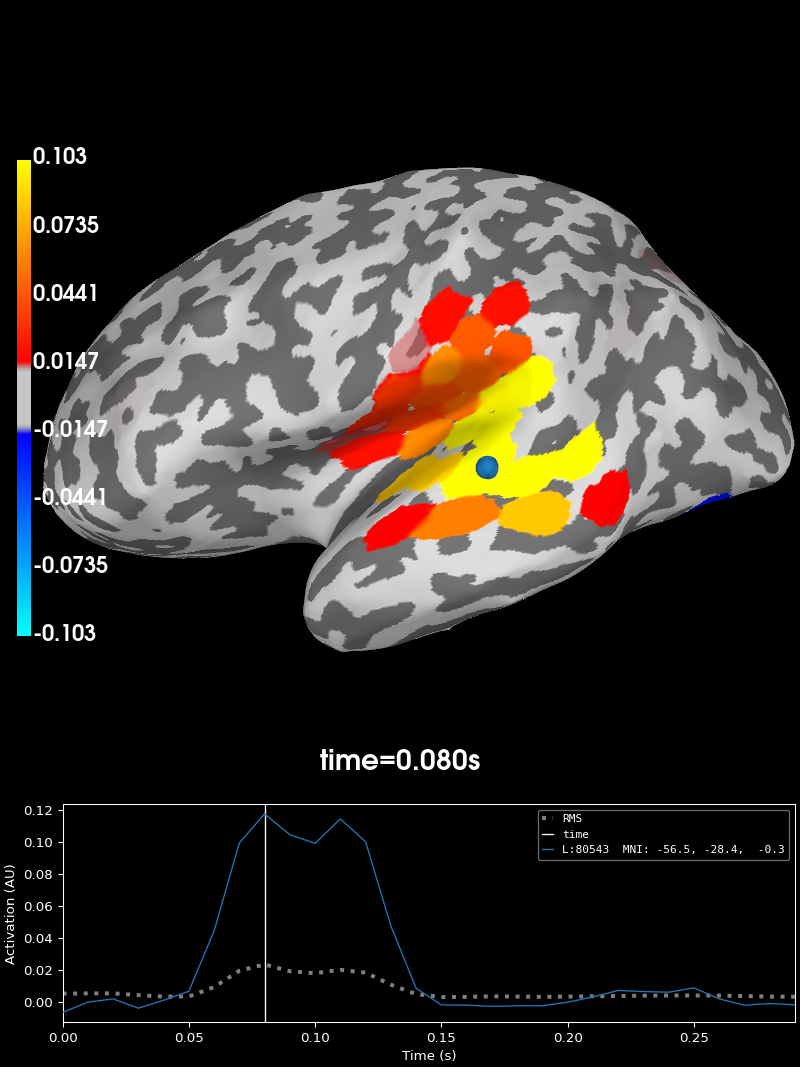
# Find the searchlight patch with highest RSA score
peak_vertex, peak_time = rsa_vals.get_peak(vert_as_index=True)
# Plot the result at the timepoint where the maximum RSA value occurs.
rsa_vals.plot("sample", subjects_dir=subjects_dir, initial_time=peak_time)
Calculating source space distances (limit=20.0 mm)...
Not adding patch information, dist_limit too small
Performing RSA between SourceEstimates and 1 model RDM(s)
Spatial radius: 0.02 meters
Using 498 vertices
Temporal radius: 2 samples
Time interval: 0-0.3 seconds
Number of searchlight patches: 14940
0%| | 0/14940 [00:00<?, ?patch/s]Creating spatio-temporal searchlight patches
0%| | 19/14940 [00:00<01:19, 187.60patch/s]
0%| | 38/14940 [00:00<01:19, 188.10patch/s]
0%| | 58/14940 [00:00<01:18, 189.08patch/s]
1%| | 78/14940 [00:00<01:18, 189.53patch/s]
1%| | 97/14940 [00:00<01:18, 188.13patch/s]
1%| | 116/14940 [00:00<01:19, 186.31patch/s]
1%| | 135/14940 [00:00<01:20, 185.01patch/s]
1%| | 154/14940 [00:00<01:20, 184.52patch/s]
1%| | 173/14940 [00:00<01:19, 184.85patch/s]
1%|▏ | 192/14940 [00:01<01:19, 185.47patch/s]
1%|▏ | 211/14940 [00:01<01:18, 186.71patch/s]
2%|▏ | 230/14940 [00:01<01:18, 187.54patch/s]
2%|▏ | 249/14940 [00:01<01:18, 188.00patch/s]
2%|▏ | 268/14940 [00:01<01:18, 188.02patch/s]
2%|▏ | 287/14940 [00:01<01:18, 187.15patch/s]
2%|▏ | 306/14940 [00:01<01:18, 186.87patch/s]
2%|▏ | 325/14940 [00:01<01:18, 186.86patch/s]
2%|▏ | 344/14940 [00:01<01:17, 187.57patch/s]
2%|▏ | 363/14940 [00:01<01:17, 187.79patch/s]
3%|▎ | 382/14940 [00:02<01:18, 186.50patch/s]
3%|▎ | 401/14940 [00:02<01:18, 185.89patch/s]
3%|▎ | 420/14940 [00:02<01:18, 185.70patch/s]
3%|▎ | 439/14940 [00:02<01:17, 186.90patch/s]
3%|▎ | 458/14940 [00:02<01:17, 187.74patch/s]
3%|▎ | 477/14940 [00:02<01:16, 188.26patch/s]
3%|▎ | 497/14940 [00:02<01:16, 188.94patch/s]
3%|▎ | 516/14940 [00:02<01:16, 188.65patch/s]
4%|▎ | 535/14940 [00:02<01:16, 187.70patch/s]
4%|▎ | 554/14940 [00:02<01:17, 186.83patch/s]
4%|▍ | 573/14940 [00:03<01:17, 186.28patch/s]
4%|▍ | 592/14940 [00:03<01:17, 186.03patch/s]
4%|▍ | 611/14940 [00:03<01:17, 185.87patch/s]
4%|▍ | 630/14940 [00:03<01:16, 185.86patch/s]
4%|▍ | 649/14940 [00:03<01:16, 185.89patch/s]
4%|▍ | 668/14940 [00:03<01:16, 185.87patch/s]
5%|▍ | 687/14940 [00:03<01:16, 185.67patch/s]
5%|▍ | 706/14940 [00:03<01:16, 185.41patch/s]
5%|▍ | 725/14940 [00:03<01:16, 185.68patch/s]
5%|▍ | 745/14940 [00:03<01:15, 186.87patch/s]
5%|▌ | 764/14940 [00:04<01:16, 186.24patch/s]
5%|▌ | 783/14940 [00:04<01:16, 185.62patch/s]
5%|▌ | 802/14940 [00:04<01:16, 185.06patch/s]
5%|▌ | 821/14940 [00:04<01:16, 184.95patch/s]
6%|▌ | 840/14940 [00:04<01:16, 185.28patch/s]
6%|▌ | 859/14940 [00:04<01:15, 185.31patch/s]
6%|▌ | 878/14940 [00:04<01:16, 184.80patch/s]
6%|▌ | 897/14940 [00:04<01:16, 183.65patch/s]
6%|▌ | 916/14940 [00:04<01:16, 183.43patch/s]
6%|▋ | 935/14940 [00:05<01:16, 183.87patch/s]
6%|▋ | 955/14940 [00:05<01:15, 185.76patch/s]
7%|▋ | 974/14940 [00:05<01:15, 185.58patch/s]
7%|▋ | 993/14940 [00:05<01:15, 185.22patch/s]
7%|▋ | 1013/14940 [00:05<01:14, 186.69patch/s]
7%|▋ | 1032/14940 [00:05<01:14, 186.28patch/s]
7%|▋ | 1051/14940 [00:05<01:14, 185.41patch/s]
7%|▋ | 1070/14940 [00:05<01:14, 186.23patch/s]
7%|▋ | 1089/14940 [00:05<01:14, 186.86patch/s]
7%|▋ | 1108/14940 [00:05<01:13, 187.77patch/s]
8%|▊ | 1127/14940 [00:06<01:13, 187.46patch/s]
8%|▊ | 1146/14940 [00:06<01:13, 187.72patch/s]
8%|▊ | 1165/14940 [00:06<01:13, 188.26patch/s]
8%|▊ | 1184/14940 [00:06<01:13, 188.11patch/s]
8%|▊ | 1203/14940 [00:06<01:12, 188.24patch/s]
8%|▊ | 1222/14940 [00:06<01:12, 188.26patch/s]
8%|▊ | 1241/14940 [00:06<01:13, 187.57patch/s]
8%|▊ | 1260/14940 [00:06<01:13, 186.87patch/s]
9%|▊ | 1279/14940 [00:06<01:13, 186.36patch/s]
9%|▊ | 1298/14940 [00:06<01:13, 185.98patch/s]
9%|▉ | 1317/14940 [00:07<01:13, 185.77patch/s]
9%|▉ | 1336/14940 [00:07<01:13, 185.65patch/s]
9%|▉ | 1355/14940 [00:07<01:13, 185.74patch/s]
9%|▉ | 1374/14940 [00:07<01:12, 186.36patch/s]
9%|▉ | 1393/14940 [00:07<01:12, 186.19patch/s]
9%|▉ | 1412/14940 [00:07<01:12, 185.79patch/s]
10%|▉ | 1431/14940 [00:07<01:13, 184.99patch/s]
10%|▉ | 1450/14940 [00:07<01:13, 184.01patch/s]
10%|▉ | 1469/14940 [00:07<01:13, 182.96patch/s]
10%|▉ | 1488/14940 [00:07<01:12, 184.75patch/s]
10%|█ | 1507/14940 [00:08<01:12, 185.59patch/s]
10%|█ | 1526/14940 [00:08<01:12, 185.54patch/s]
10%|█ | 1545/14940 [00:08<01:11, 186.15patch/s]
10%|█ | 1564/14940 [00:08<01:11, 186.44patch/s]
11%|█ | 1583/14940 [00:08<01:12, 184.72patch/s]
11%|█ | 1602/14940 [00:08<01:12, 184.80patch/s]
11%|█ | 1621/14940 [00:08<01:11, 185.54patch/s]
11%|█ | 1640/14940 [00:08<01:12, 184.18patch/s]
11%|█ | 1659/14940 [00:08<01:12, 184.20patch/s]
11%|█ | 1678/14940 [00:09<01:11, 185.26patch/s]
11%|█▏ | 1697/14940 [00:09<01:12, 183.24patch/s]
11%|█▏ | 1716/14940 [00:09<01:12, 182.23patch/s]
12%|█▏ | 1735/14940 [00:09<01:11, 183.57patch/s]
12%|█▏ | 1754/14940 [00:09<01:11, 185.16patch/s]
12%|█▏ | 1773/14940 [00:09<01:10, 185.86patch/s]
12%|█▏ | 1792/14940 [00:09<01:11, 183.45patch/s]
12%|█▏ | 1811/14940 [00:09<01:12, 181.46patch/s]
12%|█▏ | 1830/14940 [00:09<01:12, 179.88patch/s]
12%|█▏ | 1849/14940 [00:09<01:12, 181.53patch/s]
13%|█▎ | 1868/14940 [00:10<01:11, 183.16patch/s]
13%|█▎ | 1888/14940 [00:10<01:10, 185.24patch/s]
13%|█▎ | 1907/14940 [00:10<01:10, 185.54patch/s]
13%|█▎ | 1926/14940 [00:10<01:10, 185.62patch/s]
13%|█▎ | 1945/14940 [00:10<01:10, 184.36patch/s]
13%|█▎ | 1964/14940 [00:10<01:10, 183.57patch/s]
13%|█▎ | 1983/14940 [00:10<01:10, 184.66patch/s]
13%|█▎ | 2002/14940 [00:10<01:10, 184.67patch/s]
14%|█▎ | 2021/14940 [00:10<01:09, 184.61patch/s]
14%|█▎ | 2040/14940 [00:10<01:09, 184.41patch/s]
14%|█▍ | 2059/14940 [00:11<01:09, 185.36patch/s]
14%|█▍ | 2078/14940 [00:11<01:09, 185.34patch/s]
14%|█▍ | 2097/14940 [00:11<01:09, 185.41patch/s]
14%|█▍ | 2116/14940 [00:11<01:08, 186.00patch/s]
14%|█▍ | 2135/14940 [00:11<01:08, 186.26patch/s]
14%|█▍ | 2154/14940 [00:11<01:08, 186.22patch/s]
15%|█▍ | 2173/14940 [00:11<01:09, 184.00patch/s]
15%|█▍ | 2192/14940 [00:11<01:10, 181.76patch/s]
15%|█▍ | 2211/14940 [00:11<01:09, 183.93patch/s]
15%|█▍ | 2230/14940 [00:12<01:09, 183.45patch/s]
15%|█▌ | 2249/14940 [00:12<01:09, 181.68patch/s]
15%|█▌ | 2268/14940 [00:12<01:09, 183.36patch/s]
15%|█▌ | 2287/14940 [00:12<01:09, 183.34patch/s]
15%|█▌ | 2306/14940 [00:12<01:09, 180.94patch/s]
16%|█▌ | 2325/14940 [00:12<01:09, 181.63patch/s]
16%|█▌ | 2344/14940 [00:12<01:09, 182.51patch/s]
16%|█▌ | 2363/14940 [00:12<01:08, 182.70patch/s]
16%|█▌ | 2382/14940 [00:12<01:09, 181.85patch/s]
16%|█▌ | 2401/14940 [00:12<01:09, 180.53patch/s]
16%|█▌ | 2420/14940 [00:13<01:09, 179.05patch/s]
16%|█▋ | 2439/14940 [00:13<01:09, 179.72patch/s]
16%|█▋ | 2458/14940 [00:13<01:08, 182.16patch/s]
17%|█▋ | 2477/14940 [00:13<01:08, 183.14patch/s]
17%|█▋ | 2496/14940 [00:13<01:08, 182.86patch/s]
17%|█▋ | 2515/14940 [00:13<01:08, 180.71patch/s]
17%|█▋ | 2534/14940 [00:13<01:08, 181.79patch/s]
17%|█▋ | 2553/14940 [00:13<01:07, 183.27patch/s]
17%|█▋ | 2572/14940 [00:13<01:07, 184.46patch/s]
17%|█▋ | 2591/14940 [00:13<01:07, 184.11patch/s]
17%|█▋ | 2610/14940 [00:14<01:07, 182.79patch/s]
18%|█▊ | 2629/14940 [00:14<01:07, 183.42patch/s]
18%|█▊ | 2648/14940 [00:14<01:06, 184.26patch/s]
18%|█▊ | 2667/14940 [00:14<01:06, 185.27patch/s]
18%|█▊ | 2686/14940 [00:14<01:06, 185.56patch/s]
18%|█▊ | 2705/14940 [00:14<01:06, 185.32patch/s]
18%|█▊ | 2724/14940 [00:14<01:05, 185.32patch/s]
18%|█▊ | 2743/14940 [00:14<01:06, 183.61patch/s]
18%|█▊ | 2762/14940 [00:14<01:06, 181.85patch/s]
19%|█▊ | 2781/14940 [00:15<01:07, 180.69patch/s]
19%|█▊ | 2800/14940 [00:15<01:07, 180.30patch/s]
19%|█▉ | 2819/14940 [00:15<01:07, 180.57patch/s]
19%|█▉ | 2838/14940 [00:15<01:07, 180.00patch/s]
19%|█▉ | 2857/14940 [00:15<01:07, 179.87patch/s]
19%|█▉ | 2876/14940 [00:15<01:06, 180.32patch/s]
19%|█▉ | 2895/14940 [00:15<01:06, 181.18patch/s]
20%|█▉ | 2914/14940 [00:15<01:06, 181.77patch/s]
20%|█▉ | 2933/14940 [00:15<01:05, 182.29patch/s]
20%|█▉ | 2952/14940 [00:15<01:06, 181.60patch/s]
20%|█▉ | 2971/14940 [00:16<01:06, 180.59patch/s]
20%|██ | 2990/14940 [00:16<01:05, 182.14patch/s]
20%|██ | 3009/14940 [00:16<01:05, 182.54patch/s]
20%|██ | 3028/14940 [00:16<01:05, 182.20patch/s]
20%|██ | 3047/14940 [00:16<01:07, 175.25patch/s]
21%|██ | 3065/14940 [00:16<01:10, 168.61patch/s]
21%|██ | 3084/14940 [00:16<01:08, 173.38patch/s]
21%|██ | 3103/14940 [00:16<01:06, 177.35patch/s]
21%|██ | 3122/14940 [00:16<01:05, 179.99patch/s]
21%|██ | 3141/14940 [00:17<01:06, 178.74patch/s]
21%|██ | 3160/14940 [00:17<01:05, 179.40patch/s]
21%|██▏ | 3179/14940 [00:17<01:04, 181.19patch/s]
21%|██▏ | 3198/14940 [00:17<01:05, 179.79patch/s]
22%|██▏ | 3216/14940 [00:17<01:05, 179.21patch/s]
22%|██▏ | 3235/14940 [00:17<01:05, 179.71patch/s]
22%|██▏ | 3254/14940 [00:17<01:04, 180.89patch/s]
22%|██▏ | 3273/14940 [00:17<01:04, 182.17patch/s]
22%|██▏ | 3292/14940 [00:17<01:03, 182.96patch/s]
22%|██▏ | 3311/14940 [00:17<01:03, 182.35patch/s]
22%|██▏ | 3330/14940 [00:18<01:04, 180.93patch/s]
22%|██▏ | 3349/14940 [00:18<01:03, 182.27patch/s]
23%|██▎ | 3368/14940 [00:18<01:03, 183.18patch/s]
23%|██▎ | 3387/14940 [00:18<01:02, 183.77patch/s]
23%|██▎ | 3406/14940 [00:18<01:02, 184.23patch/s]
23%|██▎ | 3425/14940 [00:18<01:02, 184.55patch/s]
23%|██▎ | 3444/14940 [00:18<01:02, 184.73patch/s]
23%|██▎ | 3463/14940 [00:18<01:02, 184.42patch/s]
23%|██▎ | 3482/14940 [00:18<01:02, 183.98patch/s]
23%|██▎ | 3501/14940 [00:19<01:02, 184.32patch/s]
24%|██▎ | 3520/14940 [00:19<01:01, 184.54patch/s]
24%|██▎ | 3539/14940 [00:19<01:01, 184.83patch/s]
24%|██▍ | 3558/14940 [00:19<01:01, 184.32patch/s]
24%|██▍ | 3577/14940 [00:19<01:01, 184.12patch/s]
24%|██▍ | 3596/14940 [00:19<01:01, 184.43patch/s]
24%|██▍ | 3615/14940 [00:19<01:01, 184.65patch/s]
24%|██▍ | 3634/14940 [00:19<01:01, 184.16patch/s]
24%|██▍ | 3653/14940 [00:19<01:02, 181.61patch/s]
25%|██▍ | 3672/14940 [00:19<01:02, 181.60patch/s]
25%|██▍ | 3691/14940 [00:20<01:01, 182.33patch/s]
25%|██▍ | 3710/14940 [00:20<01:02, 180.07patch/s]
25%|██▍ | 3729/14940 [00:20<01:02, 179.14patch/s]
25%|██▌ | 3747/14940 [00:20<01:02, 178.90patch/s]
25%|██▌ | 3766/14940 [00:20<01:02, 179.70patch/s]
25%|██▌ | 3785/14940 [00:20<01:01, 181.18patch/s]
25%|██▌ | 3804/14940 [00:20<01:01, 181.65patch/s]
26%|██▌ | 3823/14940 [00:20<01:01, 180.86patch/s]
26%|██▌ | 3842/14940 [00:20<01:01, 180.58patch/s]
26%|██▌ | 3861/14940 [00:20<01:01, 181.01patch/s]
26%|██▌ | 3880/14940 [00:21<01:01, 180.55patch/s]
26%|██▌ | 3899/14940 [00:21<01:01, 180.43patch/s]
26%|██▌ | 3918/14940 [00:21<01:01, 179.16patch/s]
26%|██▋ | 3936/14940 [00:21<01:01, 178.36patch/s]
26%|██▋ | 3954/14940 [00:21<01:01, 177.95patch/s]
27%|██▋ | 3972/14940 [00:21<01:01, 177.93patch/s]
27%|██▋ | 3990/14940 [00:21<01:01, 177.74patch/s]
27%|██▋ | 4009/14940 [00:21<01:00, 179.61patch/s]
27%|██▋ | 4028/14940 [00:21<01:00, 181.29patch/s]
27%|██▋ | 4047/14940 [00:22<00:59, 182.46patch/s]
27%|██▋ | 4066/14940 [00:22<00:59, 183.47patch/s]
27%|██▋ | 4085/14940 [00:22<00:58, 184.15patch/s]
27%|██▋ | 4104/14940 [00:22<00:58, 184.64patch/s]
28%|██▊ | 4123/14940 [00:22<00:58, 184.88patch/s]
28%|██▊ | 4142/14940 [00:22<00:58, 184.89patch/s]
28%|██▊ | 4161/14940 [00:22<00:58, 183.61patch/s]
28%|██▊ | 4180/14940 [00:22<00:58, 183.22patch/s]
28%|██▊ | 4199/14940 [00:22<00:58, 183.40patch/s]
28%|██▊ | 4218/14940 [00:22<00:58, 184.00patch/s]
28%|██▊ | 4237/14940 [00:23<00:58, 184.14patch/s]
28%|██▊ | 4256/14940 [00:23<00:58, 182.88patch/s]
29%|██▊ | 4275/14940 [00:23<00:58, 180.80patch/s]
29%|██▊ | 4294/14940 [00:23<00:59, 180.12patch/s]
29%|██▉ | 4313/14940 [00:23<00:58, 182.52patch/s]
29%|██▉ | 4332/14940 [00:23<00:58, 182.28patch/s]
29%|██▉ | 4351/14940 [00:23<00:58, 181.05patch/s]
29%|██▉ | 4370/14940 [00:23<00:58, 179.75patch/s]
29%|██▉ | 4389/14940 [00:23<00:58, 180.61patch/s]
30%|██▉ | 4408/14940 [00:24<00:57, 182.94patch/s]
30%|██▉ | 4427/14940 [00:24<00:57, 183.68patch/s]
30%|██▉ | 4446/14940 [00:24<00:57, 183.92patch/s]
30%|██▉ | 4465/14940 [00:24<00:56, 184.44patch/s]
30%|███ | 4484/14940 [00:24<00:56, 184.82patch/s]
30%|███ | 4503/14940 [00:24<00:56, 185.19patch/s]
30%|███ | 4522/14940 [00:24<00:55, 186.05patch/s]
30%|███ | 4541/14940 [00:24<00:56, 184.36patch/s]
31%|███ | 4560/14940 [00:24<00:57, 181.91patch/s]
31%|███ | 4579/14940 [00:24<00:56, 182.42patch/s]
31%|███ | 4598/14940 [00:25<00:56, 182.77patch/s]
31%|███ | 4617/14940 [00:25<00:56, 183.07patch/s]
31%|███ | 4636/14940 [00:25<00:56, 183.52patch/s]
31%|███ | 4655/14940 [00:25<00:55, 184.23patch/s]
31%|███▏ | 4674/14940 [00:25<00:55, 184.54patch/s]
31%|███▏ | 4693/14940 [00:25<00:55, 183.85patch/s]
32%|███▏ | 4712/14940 [00:25<00:55, 182.92patch/s]
32%|███▏ | 4731/14940 [00:25<00:56, 181.42patch/s]
32%|███▏ | 4750/14940 [00:25<00:56, 181.61patch/s]
32%|███▏ | 4769/14940 [00:25<00:55, 182.71patch/s]
32%|███▏ | 4788/14940 [00:26<00:55, 182.61patch/s]
32%|███▏ | 4807/14940 [00:26<00:55, 183.97patch/s]
32%|███▏ | 4826/14940 [00:26<00:54, 184.60patch/s]
32%|███▏ | 4845/14940 [00:26<00:55, 183.24patch/s]
33%|███▎ | 4864/14940 [00:26<00:55, 182.59patch/s]
33%|███▎ | 4883/14940 [00:26<00:54, 184.71patch/s]
33%|███▎ | 4902/14940 [00:26<00:54, 185.86patch/s]
33%|███▎ | 4921/14940 [00:26<00:53, 186.54patch/s]
33%|███▎ | 4940/14940 [00:26<00:53, 186.23patch/s]
33%|███▎ | 4959/14940 [00:26<00:53, 185.98patch/s]
33%|███▎ | 4978/14940 [00:27<00:53, 185.63patch/s]
33%|███▎ | 4997/14940 [00:27<00:53, 185.55patch/s]
34%|███▎ | 5016/14940 [00:27<00:53, 185.65patch/s]
34%|███▎ | 5035/14940 [00:27<00:53, 186.28patch/s]
34%|███▍ | 5054/14940 [00:27<00:52, 186.74patch/s]
34%|███▍ | 5073/14940 [00:27<00:52, 187.01patch/s]
34%|███▍ | 5092/14940 [00:27<00:52, 187.42patch/s]
34%|███▍ | 5111/14940 [00:27<00:52, 186.32patch/s]
34%|███▍ | 5130/14940 [00:27<00:53, 184.64patch/s]
34%|███▍ | 5149/14940 [00:28<00:52, 185.97patch/s]
35%|███▍ | 5168/14940 [00:28<00:52, 185.78patch/s]
35%|███▍ | 5187/14940 [00:28<00:52, 184.19patch/s]
35%|███▍ | 5206/14940 [00:28<00:52, 184.34patch/s]
35%|███▍ | 5225/14940 [00:28<00:52, 184.63patch/s]
35%|███▌ | 5244/14940 [00:28<00:52, 184.93patch/s]
35%|███▌ | 5263/14940 [00:28<00:52, 185.02patch/s]
35%|███▌ | 5282/14940 [00:28<00:52, 185.27patch/s]
35%|███▌ | 5301/14940 [00:28<00:51, 186.16patch/s]
36%|███▌ | 5320/14940 [00:28<00:51, 185.36patch/s]
36%|███▌ | 5339/14940 [00:29<00:52, 184.04patch/s]
36%|███▌ | 5358/14940 [00:29<00:51, 185.09patch/s]
36%|███▌ | 5377/14940 [00:29<00:51, 186.12patch/s]
36%|███▌ | 5396/14940 [00:29<00:51, 187.10patch/s]
36%|███▌ | 5415/14940 [00:29<00:50, 186.89patch/s]
36%|███▋ | 5434/14940 [00:29<00:50, 186.64patch/s]
36%|███▋ | 5453/14940 [00:29<00:50, 187.05patch/s]
37%|███▋ | 5472/14940 [00:29<00:50, 186.70patch/s]
37%|███▋ | 5491/14940 [00:29<00:50, 186.14patch/s]
37%|███▋ | 5510/14940 [00:29<00:50, 185.24patch/s]
37%|███▋ | 5529/14940 [00:30<00:50, 185.37patch/s]
37%|███▋ | 5548/14940 [00:30<00:50, 186.61patch/s]
37%|███▋ | 5567/14940 [00:30<00:50, 186.36patch/s]
37%|███▋ | 5586/14940 [00:30<00:50, 186.40patch/s]
38%|███▊ | 5605/14940 [00:30<00:49, 187.04patch/s]
38%|███▊ | 5624/14940 [00:30<00:49, 187.65patch/s]
38%|███▊ | 5643/14940 [00:30<00:49, 188.02patch/s]
38%|███▊ | 5662/14940 [00:30<00:49, 186.55patch/s]
38%|███▊ | 5681/14940 [00:30<00:49, 185.61patch/s]
38%|███▊ | 5700/14940 [00:30<00:49, 185.10patch/s]
38%|███▊ | 5719/14940 [00:31<00:49, 186.42patch/s]
38%|███▊ | 5738/14940 [00:31<00:49, 187.26patch/s]
39%|███▊ | 5757/14940 [00:31<00:48, 187.60patch/s]
39%|███▊ | 5776/14940 [00:31<00:48, 188.21patch/s]
39%|███▉ | 5795/14940 [00:31<00:48, 188.53patch/s]
39%|███▉ | 5814/14940 [00:31<00:48, 187.62patch/s]
39%|███▉ | 5833/14940 [00:31<00:48, 187.57patch/s]
39%|███▉ | 5852/14940 [00:31<00:48, 187.65patch/s]
39%|███▉ | 5871/14940 [00:31<00:48, 187.75patch/s]
39%|███▉ | 5890/14940 [00:31<00:48, 187.13patch/s]
40%|███▉ | 5909/14940 [00:32<00:48, 186.08patch/s]
40%|███▉ | 5928/14940 [00:32<00:48, 185.95patch/s]
40%|███▉ | 5947/14940 [00:32<00:48, 185.81patch/s]
40%|███▉ | 5966/14940 [00:32<00:48, 185.84patch/s]
40%|████ | 5985/14940 [00:32<00:48, 185.14patch/s]
40%|████ | 6004/14940 [00:32<00:48, 184.69patch/s]
40%|████ | 6023/14940 [00:32<00:48, 184.34patch/s]
40%|████ | 6042/14940 [00:32<00:48, 184.53patch/s]
41%|████ | 6061/14940 [00:32<00:47, 185.04patch/s]
41%|████ | 6080/14940 [00:33<00:47, 185.98patch/s]
41%|████ | 6099/14940 [00:33<00:47, 186.65patch/s]
41%|████ | 6118/14940 [00:33<00:47, 187.20patch/s]
41%|████ | 6137/14940 [00:33<00:46, 187.95patch/s]
41%|████ | 6156/14940 [00:33<00:46, 188.07patch/s]
41%|████▏ | 6175/14940 [00:33<00:46, 187.39patch/s]
41%|████▏ | 6194/14940 [00:33<00:46, 187.38patch/s]
42%|████▏ | 6213/14940 [00:33<00:46, 187.46patch/s]
42%|████▏ | 6232/14940 [00:33<00:46, 186.40patch/s]
42%|████▏ | 6251/14940 [00:33<00:46, 186.30patch/s]
42%|████▏ | 6270/14940 [00:34<00:46, 186.92patch/s]
42%|████▏ | 6289/14940 [00:34<00:46, 185.92patch/s]
42%|████▏ | 6308/14940 [00:34<00:46, 185.56patch/s]
42%|████▏ | 6327/14940 [00:34<00:46, 186.45patch/s]
42%|████▏ | 6346/14940 [00:34<00:46, 186.35patch/s]
43%|████▎ | 6365/14940 [00:34<00:46, 186.35patch/s]
43%|████▎ | 6384/14940 [00:34<00:45, 186.95patch/s]
43%|████▎ | 6403/14940 [00:34<00:45, 187.59patch/s]
43%|████▎ | 6422/14940 [00:34<00:45, 188.13patch/s]
43%|████▎ | 6441/14940 [00:34<00:45, 186.90patch/s]
43%|████▎ | 6460/14940 [00:35<00:45, 186.90patch/s]
43%|████▎ | 6479/14940 [00:35<00:45, 187.74patch/s]
43%|████▎ | 6498/14940 [00:35<00:44, 188.37patch/s]
44%|████▎ | 6517/14940 [00:35<00:44, 188.62patch/s]
44%|████▎ | 6536/14940 [00:35<00:44, 188.59patch/s]
44%|████▍ | 6555/14940 [00:35<00:44, 187.82patch/s]
44%|████▍ | 6574/14940 [00:35<00:44, 187.35patch/s]
44%|████▍ | 6593/14940 [00:35<00:44, 187.99patch/s]
44%|████▍ | 6612/14940 [00:35<00:44, 187.21patch/s]
44%|████▍ | 6631/14940 [00:35<00:44, 186.18patch/s]
45%|████▍ | 6650/14940 [00:36<00:44, 185.19patch/s]
45%|████▍ | 6669/14940 [00:36<00:44, 184.94patch/s]
45%|████▍ | 6688/14940 [00:36<00:44, 185.20patch/s]
45%|████▍ | 6707/14940 [00:36<00:44, 185.91patch/s]
45%|████▌ | 6726/14940 [00:36<00:44, 186.50patch/s]
45%|████▌ | 6745/14940 [00:36<00:43, 186.96patch/s]
45%|████▌ | 6764/14940 [00:36<00:43, 187.05patch/s]
45%|████▌ | 6783/14940 [00:36<00:43, 187.34patch/s]
46%|████▌ | 6802/14940 [00:36<00:43, 187.55patch/s]
46%|████▌ | 6821/14940 [00:36<00:43, 188.13patch/s]
46%|████▌ | 6840/14940 [00:37<00:42, 188.42patch/s]
46%|████▌ | 6859/14940 [00:37<00:42, 188.02patch/s]
46%|████▌ | 6878/14940 [00:37<00:42, 187.80patch/s]
46%|████▌ | 6897/14940 [00:37<00:42, 187.81patch/s]
46%|████▋ | 6916/14940 [00:37<00:42, 188.02patch/s]
46%|████▋ | 6935/14940 [00:37<00:42, 188.36patch/s]
47%|████▋ | 6954/14940 [00:37<00:42, 188.63patch/s]
47%|████▋ | 6973/14940 [00:37<00:42, 188.03patch/s]
47%|████▋ | 6992/14940 [00:37<00:42, 187.35patch/s]
47%|████▋ | 7012/14940 [00:37<00:42, 188.20patch/s]
47%|████▋ | 7031/14940 [00:38<00:42, 187.94patch/s]
47%|████▋ | 7050/14940 [00:38<00:42, 187.18patch/s]
47%|████▋ | 7069/14940 [00:38<00:42, 186.69patch/s]
47%|████▋ | 7088/14940 [00:38<00:42, 186.94patch/s]
48%|████▊ | 7107/14940 [00:38<00:41, 187.74patch/s]
48%|████▊ | 7126/14940 [00:38<00:41, 188.41patch/s]
48%|████▊ | 7145/14940 [00:38<00:41, 188.78patch/s]
48%|████▊ | 7165/14940 [00:38<00:41, 189.20patch/s]
48%|████▊ | 7184/14940 [00:38<00:41, 189.04patch/s]
48%|████▊ | 7203/14940 [00:39<00:40, 188.78patch/s]
48%|████▊ | 7222/14940 [00:39<00:40, 188.46patch/s]
48%|████▊ | 7241/14940 [00:39<00:40, 188.60patch/s]
49%|████▊ | 7260/14940 [00:39<00:40, 188.96patch/s]
49%|████▊ | 7279/14940 [00:39<00:40, 188.80patch/s]
49%|████▉ | 7298/14940 [00:39<00:40, 188.64patch/s]
49%|████▉ | 7317/14940 [00:39<00:40, 188.35patch/s]
49%|████▉ | 7336/14940 [00:39<00:40, 188.74patch/s]
49%|████▉ | 7355/14940 [00:39<00:40, 188.97patch/s]
49%|████▉ | 7374/14940 [00:39<00:40, 188.72patch/s]
49%|████▉ | 7393/14940 [00:40<00:39, 188.87patch/s]
50%|████▉ | 7412/14940 [00:40<00:39, 188.91patch/s]
50%|████▉ | 7431/14940 [00:40<00:39, 188.05patch/s]
50%|████▉ | 7450/14940 [00:40<00:39, 188.00patch/s]
50%|█████ | 7470/14940 [00:40<00:39, 188.74patch/s]
50%|█████ | 7489/14940 [00:40<00:39, 188.75patch/s]
50%|█████ | 7508/14940 [00:40<00:39, 188.68patch/s]
50%|█████ | 7527/14940 [00:40<00:39, 188.97patch/s]
51%|█████ | 7546/14940 [00:40<00:39, 188.57patch/s]
51%|█████ | 7565/14940 [00:40<00:39, 188.26patch/s]
51%|█████ | 7584/14940 [00:41<00:39, 187.49patch/s]
51%|█████ | 7603/14940 [00:41<00:39, 187.31patch/s]
51%|█████ | 7622/14940 [00:41<00:38, 187.66patch/s]
51%|█████ | 7642/14940 [00:41<00:38, 188.54patch/s]
51%|█████▏ | 7662/14940 [00:41<00:38, 189.09patch/s]
51%|█████▏ | 7681/14940 [00:41<00:38, 189.31patch/s]
52%|█████▏ | 7700/14940 [00:41<00:38, 188.25patch/s]
52%|█████▏ | 7719/14940 [00:41<00:38, 187.50patch/s]
52%|█████▏ | 7738/14940 [00:41<00:38, 186.97patch/s]
52%|█████▏ | 7757/14940 [00:41<00:38, 187.30patch/s]
52%|█████▏ | 7776/14940 [00:42<00:38, 187.27patch/s]
52%|█████▏ | 7795/14940 [00:42<00:38, 186.84patch/s]
52%|█████▏ | 7814/14940 [00:42<00:38, 187.13patch/s]
52%|█████▏ | 7833/14940 [00:42<00:37, 187.41patch/s]
53%|█████▎ | 7852/14940 [00:42<00:37, 186.88patch/s]
53%|█████▎ | 7871/14940 [00:42<00:38, 185.80patch/s]
53%|█████▎ | 7890/14940 [00:42<00:38, 184.97patch/s]
53%|█████▎ | 7909/14940 [00:42<00:37, 185.77patch/s]
53%|█████▎ | 7928/14940 [00:42<00:37, 186.50patch/s]
53%|█████▎ | 7947/14940 [00:42<00:37, 187.18patch/s]
53%|█████▎ | 7966/14940 [00:43<00:37, 186.39patch/s]
53%|█████▎ | 7985/14940 [00:43<00:37, 185.68patch/s]
54%|█████▎ | 8004/14940 [00:43<00:37, 185.77patch/s]
54%|█████▎ | 8023/14940 [00:43<00:37, 186.65patch/s]
54%|█████▍ | 8042/14940 [00:43<00:36, 187.50patch/s]
54%|█████▍ | 8061/14940 [00:43<00:36, 187.71patch/s]
54%|█████▍ | 8080/14940 [00:43<00:36, 186.80patch/s]
54%|█████▍ | 8099/14940 [00:43<00:36, 184.92patch/s]
54%|█████▍ | 8118/14940 [00:43<00:36, 185.02patch/s]
54%|█████▍ | 8137/14940 [00:43<00:36, 185.75patch/s]
55%|█████▍ | 8156/14940 [00:44<00:36, 186.90patch/s]
55%|█████▍ | 8175/14940 [00:44<00:36, 186.14patch/s]
55%|█████▍ | 8194/14940 [00:44<00:36, 185.10patch/s]
55%|█████▍ | 8213/14940 [00:44<00:36, 184.72patch/s]
55%|█████▌ | 8232/14940 [00:44<00:36, 184.86patch/s]
55%|█████▌ | 8251/14940 [00:44<00:36, 185.10patch/s]
55%|█████▌ | 8270/14940 [00:44<00:36, 184.69patch/s]
55%|█████▌ | 8289/14940 [00:44<00:35, 185.36patch/s]
56%|█████▌ | 8309/14940 [00:44<00:35, 186.86patch/s]
56%|█████▌ | 8329/14940 [00:45<00:35, 187.87patch/s]
56%|█████▌ | 8348/14940 [00:45<00:34, 188.42patch/s]
56%|█████▌ | 8368/14940 [00:45<00:34, 189.00patch/s]
56%|█████▌ | 8387/14940 [00:45<00:34, 189.19patch/s]
56%|█████▋ | 8406/14940 [00:45<00:34, 189.24patch/s]
56%|█████▋ | 8425/14940 [00:45<00:34, 188.94patch/s]
57%|█████▋ | 8444/14940 [00:45<00:34, 187.53patch/s]
57%|█████▋ | 8463/14940 [00:45<00:34, 186.51patch/s]
57%|█████▋ | 8482/14940 [00:45<00:34, 186.87patch/s]
57%|█████▋ | 8501/14940 [00:45<00:34, 187.23patch/s]
57%|█████▋ | 8520/14940 [00:46<00:34, 187.37patch/s]
57%|█████▋ | 8539/14940 [00:46<00:34, 186.81patch/s]
57%|█████▋ | 8558/14940 [00:46<00:34, 186.48patch/s]
57%|█████▋ | 8577/14940 [00:46<00:34, 186.26patch/s]
58%|█████▊ | 8596/14940 [00:46<00:34, 184.95patch/s]
58%|█████▊ | 8615/14940 [00:46<00:34, 184.18patch/s]
58%|█████▊ | 8634/14940 [00:46<00:34, 184.66patch/s]
58%|█████▊ | 8653/14940 [00:46<00:34, 184.70patch/s]
58%|█████▊ | 8672/14940 [00:46<00:33, 185.14patch/s]
58%|█████▊ | 8692/14940 [00:46<00:33, 186.63patch/s]
58%|█████▊ | 8711/14940 [00:47<00:33, 186.71patch/s]
58%|█████▊ | 8730/14940 [00:47<00:33, 186.52patch/s]
59%|█████▊ | 8749/14940 [00:47<00:33, 185.64patch/s]
59%|█████▊ | 8768/14940 [00:47<00:33, 185.23patch/s]
59%|█████▉ | 8787/14940 [00:47<00:33, 185.40patch/s]
59%|█████▉ | 8806/14940 [00:47<00:33, 185.49patch/s]
59%|█████▉ | 8825/14940 [00:47<00:32, 185.86patch/s]
59%|█████▉ | 8844/14940 [00:47<00:32, 187.06patch/s]
59%|█████▉ | 8863/14940 [00:47<00:32, 187.82patch/s]
59%|█████▉ | 8882/14940 [00:47<00:32, 188.13patch/s]
60%|█████▉ | 8901/14940 [00:48<00:32, 185.94patch/s]
60%|█████▉ | 8920/14940 [00:48<00:32, 184.96patch/s]
60%|█████▉ | 8939/14940 [00:48<00:32, 184.56patch/s]
60%|█████▉ | 8958/14940 [00:48<00:32, 186.07patch/s]
60%|██████ | 8977/14940 [00:48<00:31, 187.09patch/s]
60%|██████ | 8996/14940 [00:48<00:31, 187.49patch/s]
60%|██████ | 9015/14940 [00:48<00:31, 187.74patch/s]
60%|██████ | 9034/14940 [00:48<00:31, 188.06patch/s]
61%|██████ | 9054/14940 [00:48<00:31, 188.73patch/s]
61%|██████ | 9073/14940 [00:49<00:31, 188.26patch/s]
61%|██████ | 9092/14940 [00:49<00:31, 187.56patch/s]
61%|██████ | 9111/14940 [00:49<00:31, 187.85patch/s]
61%|██████ | 9130/14940 [00:49<00:30, 188.30patch/s]
61%|██████ | 9150/14940 [00:49<00:30, 188.84patch/s]
61%|██████▏ | 9169/14940 [00:49<00:31, 185.73patch/s]
61%|██████▏ | 9188/14940 [00:49<00:31, 184.38patch/s]
62%|██████▏ | 9207/14940 [00:49<00:31, 184.83patch/s]
62%|██████▏ | 9226/14940 [00:49<00:30, 185.75patch/s]
62%|██████▏ | 9245/14940 [00:49<00:30, 186.28patch/s]
62%|██████▏ | 9264/14940 [00:50<00:30, 186.09patch/s]
62%|██████▏ | 9283/14940 [00:50<00:30, 185.58patch/s]
62%|██████▏ | 9302/14940 [00:50<00:30, 185.41patch/s]
62%|██████▏ | 9321/14940 [00:50<00:30, 183.99patch/s]
63%|██████▎ | 9340/14940 [00:50<00:30, 184.31patch/s]
63%|██████▎ | 9360/14940 [00:50<00:29, 186.11patch/s]
63%|██████▎ | 9379/14940 [00:50<00:29, 186.06patch/s]
63%|██████▎ | 9398/14940 [00:50<00:29, 185.65patch/s]
63%|██████▎ | 9417/14940 [00:50<00:29, 185.59patch/s]
63%|██████▎ | 9436/14940 [00:50<00:29, 186.74patch/s]
63%|██████▎ | 9455/14940 [00:51<00:29, 187.33patch/s]
63%|██████▎ | 9474/14940 [00:51<00:29, 186.78patch/s]
64%|██████▎ | 9493/14940 [00:51<00:29, 184.46patch/s]
64%|██████▎ | 9512/14940 [00:51<00:29, 182.39patch/s]
64%|██████▍ | 9531/14940 [00:51<00:29, 184.12patch/s]
64%|██████▍ | 9550/14940 [00:51<00:29, 184.32patch/s]
64%|██████▍ | 9569/14940 [00:51<00:29, 183.36patch/s]
64%|██████▍ | 9588/14940 [00:51<00:29, 184.01patch/s]
64%|██████▍ | 9607/14940 [00:51<00:28, 184.49patch/s]
64%|██████▍ | 9626/14940 [00:51<00:28, 184.93patch/s]
65%|██████▍ | 9645/14940 [00:52<00:28, 185.79patch/s]
65%|██████▍ | 9664/14940 [00:52<00:28, 186.35patch/s]
65%|██████▍ | 9683/14940 [00:52<00:28, 185.47patch/s]
65%|██████▍ | 9702/14940 [00:52<00:28, 183.23patch/s]
65%|██████▌ | 9721/14940 [00:52<00:28, 181.02patch/s]
65%|██████▌ | 9740/14940 [00:52<00:28, 180.03patch/s]
65%|██████▌ | 9759/14940 [00:52<00:28, 180.71patch/s]
65%|██████▌ | 9778/14940 [00:52<00:28, 182.90patch/s]
66%|██████▌ | 9797/14940 [00:52<00:27, 183.70patch/s]
66%|██████▌ | 9816/14940 [00:53<00:27, 184.12patch/s]
66%|██████▌ | 9835/14940 [00:53<00:27, 183.96patch/s]
66%|██████▌ | 9854/14940 [00:53<00:27, 184.91patch/s]
66%|██████▌ | 9873/14940 [00:53<00:27, 186.02patch/s]
66%|██████▌ | 9892/14940 [00:53<00:26, 187.15patch/s]
66%|██████▋ | 9912/14940 [00:53<00:26, 188.06patch/s]
66%|██████▋ | 9931/14940 [00:53<00:26, 188.31patch/s]
67%|██████▋ | 9950/14940 [00:53<00:27, 184.54patch/s]
67%|██████▋ | 9969/14940 [00:53<00:27, 183.28patch/s]
67%|██████▋ | 9988/14940 [00:53<00:26, 183.95patch/s]
67%|██████▋ | 10007/14940 [00:54<00:26, 184.21patch/s]
67%|██████▋ | 10026/14940 [00:54<00:26, 184.63patch/s]
67%|██████▋ | 10045/14940 [00:54<00:26, 184.65patch/s]
67%|██████▋ | 10064/14940 [00:54<00:26, 184.77patch/s]
67%|██████▋ | 10083/14940 [00:54<00:26, 184.66patch/s]
68%|██████▊ | 10102/14940 [00:54<00:26, 182.86patch/s]
68%|██████▊ | 10121/14940 [00:54<00:26, 180.98patch/s]
68%|██████▊ | 10140/14940 [00:54<00:26, 179.65patch/s]
68%|██████▊ | 10159/14940 [00:54<00:26, 181.37patch/s]
68%|██████▊ | 10178/14940 [00:54<00:26, 183.06patch/s]
68%|██████▊ | 10197/14940 [00:55<00:25, 184.42patch/s]
68%|██████▊ | 10216/14940 [00:55<00:25, 185.03patch/s]
69%|██████▊ | 10235/14940 [00:55<00:25, 184.39patch/s]
69%|██████▊ | 10254/14940 [00:55<00:25, 181.70patch/s]
69%|██████▉ | 10273/14940 [00:55<00:25, 179.95patch/s]
69%|██████▉ | 10292/14940 [00:55<00:25, 178.92patch/s]
69%|██████▉ | 10311/14940 [00:55<00:25, 179.65patch/s]
69%|██████▉ | 10329/14940 [00:55<00:25, 179.66patch/s]
69%|██████▉ | 10347/14940 [00:55<00:25, 179.38patch/s]
69%|██████▉ | 10366/14940 [00:56<00:25, 180.98patch/s]
70%|██████▉ | 10385/14940 [00:56<00:25, 182.02patch/s]
70%|██████▉ | 10404/14940 [00:56<00:24, 182.58patch/s]
70%|██████▉ | 10423/14940 [00:56<00:24, 183.34patch/s]
70%|██████▉ | 10442/14940 [00:56<00:24, 184.33patch/s]
70%|███████ | 10462/14940 [00:56<00:24, 186.09patch/s]
70%|███████ | 10481/14940 [00:56<00:24, 184.64patch/s]
70%|███████ | 10500/14940 [00:56<00:24, 181.94patch/s]
70%|███████ | 10519/14940 [00:56<00:24, 180.92patch/s]
71%|███████ | 10538/14940 [00:56<00:24, 181.12patch/s]
71%|███████ | 10557/14940 [00:57<00:24, 182.45patch/s]
71%|███████ | 10576/14940 [00:57<00:23, 182.91patch/s]
71%|███████ | 10595/14940 [00:57<00:23, 182.74patch/s]
71%|███████ | 10614/14940 [00:57<00:23, 181.49patch/s]
71%|███████ | 10633/14940 [00:57<00:23, 181.61patch/s]
71%|███████▏ | 10652/14940 [00:57<00:23, 182.01patch/s]
71%|███████▏ | 10671/14940 [00:57<00:23, 180.87patch/s]
72%|███████▏ | 10690/14940 [00:57<00:23, 180.94patch/s]
72%|███████▏ | 10709/14940 [00:57<00:23, 181.77patch/s]
72%|███████▏ | 10728/14940 [00:58<00:23, 180.06patch/s]
72%|███████▏ | 10747/14940 [00:58<00:23, 178.81patch/s]
72%|███████▏ | 10765/14940 [00:58<00:23, 178.14patch/s]
72%|███████▏ | 10783/14940 [00:58<00:23, 177.61patch/s]
72%|███████▏ | 10801/14940 [00:58<00:23, 177.29patch/s]
72%|███████▏ | 10820/14940 [00:58<00:23, 178.61patch/s]
73%|███████▎ | 10839/14940 [00:58<00:22, 180.02patch/s]
73%|███████▎ | 10858/14940 [00:58<00:22, 181.69patch/s]
73%|███████▎ | 10877/14940 [00:58<00:22, 182.93patch/s]
73%|███████▎ | 10896/14940 [00:58<00:22, 183.80patch/s]
73%|███████▎ | 10915/14940 [00:59<00:21, 184.21patch/s]
73%|███████▎ | 10934/14940 [00:59<00:21, 184.68patch/s]
73%|███████▎ | 10953/14940 [00:59<00:21, 184.95patch/s]
73%|███████▎ | 10972/14940 [00:59<00:21, 185.18patch/s]
74%|███████▎ | 10991/14940 [00:59<00:21, 185.33patch/s]
74%|███████▎ | 11010/14940 [00:59<00:21, 185.49patch/s]
74%|███████▍ | 11029/14940 [00:59<00:21, 182.55patch/s]
74%|███████▍ | 11048/14940 [00:59<00:21, 180.92patch/s]
74%|███████▍ | 11067/14940 [00:59<00:21, 180.29patch/s]
74%|███████▍ | 11086/14940 [00:59<00:21, 182.11patch/s]
74%|███████▍ | 11105/14940 [01:00<00:20, 183.81patch/s]
74%|███████▍ | 11124/14940 [01:00<00:20, 185.17patch/s]
75%|███████▍ | 11143/14940 [01:00<00:20, 184.67patch/s]
75%|███████▍ | 11162/14940 [01:00<00:20, 183.65patch/s]
75%|███████▍ | 11181/14940 [01:00<00:20, 183.64patch/s]
75%|███████▍ | 11200/14940 [01:00<00:20, 184.64patch/s]
75%|███████▌ | 11219/14940 [01:00<00:19, 186.19patch/s]
75%|███████▌ | 11238/14940 [01:00<00:19, 185.81patch/s]
75%|███████▌ | 11257/14940 [01:00<00:19, 185.83patch/s]
75%|███████▌ | 11276/14940 [01:01<00:19, 185.76patch/s]
76%|███████▌ | 11295/14940 [01:01<00:19, 185.03patch/s]
76%|███████▌ | 11314/14940 [01:01<00:19, 184.48patch/s]
76%|███████▌ | 11333/14940 [01:01<00:19, 184.29patch/s]
76%|███████▌ | 11352/14940 [01:01<00:19, 184.48patch/s]
76%|███████▌ | 11371/14940 [01:01<00:19, 184.75patch/s]
76%|███████▌ | 11390/14940 [01:01<00:19, 182.86patch/s]
76%|███████▋ | 11409/14940 [01:01<00:19, 182.52patch/s]
76%|███████▋ | 11428/14940 [01:01<00:19, 183.42patch/s]
77%|███████▋ | 11447/14940 [01:01<00:18, 184.07patch/s]
77%|███████▋ | 11466/14940 [01:02<00:18, 184.03patch/s]
77%|███████▋ | 11485/14940 [01:02<00:18, 183.28patch/s]
77%|███████▋ | 11504/14940 [01:02<00:18, 182.56patch/s]
77%|███████▋ | 11523/14940 [01:02<00:18, 181.77patch/s]
77%|███████▋ | 11542/14940 [01:02<00:18, 179.99patch/s]
77%|███████▋ | 11561/14940 [01:02<00:18, 179.72patch/s]
78%|███████▊ | 11580/14940 [01:02<00:18, 180.17patch/s]
78%|███████▊ | 11599/14940 [01:02<00:18, 179.66patch/s]
78%|███████▊ | 11618/14940 [01:02<00:18, 180.19patch/s]
78%|███████▊ | 11637/14940 [01:02<00:18, 181.81patch/s]
78%|███████▊ | 11656/14940 [01:03<00:17, 182.93patch/s]
78%|███████▊ | 11675/14940 [01:03<00:17, 183.69patch/s]
78%|███████▊ | 11694/14940 [01:03<00:17, 184.38patch/s]
78%|███████▊ | 11713/14940 [01:03<00:17, 183.30patch/s]
79%|███████▊ | 11732/14940 [01:03<00:17, 181.65patch/s]
79%|███████▊ | 11751/14940 [01:03<00:17, 181.98patch/s]
79%|███████▉ | 11770/14940 [01:03<00:17, 181.89patch/s]
79%|███████▉ | 11789/14940 [01:03<00:17, 182.26patch/s]
79%|███████▉ | 11808/14940 [01:03<00:17, 183.17patch/s]
79%|███████▉ | 11827/14940 [01:04<00:16, 183.49patch/s]
79%|███████▉ | 11846/14940 [01:04<00:16, 182.70patch/s]
79%|███████▉ | 11865/14940 [01:04<00:16, 183.73patch/s]
80%|███████▉ | 11884/14940 [01:04<00:16, 184.86patch/s]
80%|███████▉ | 11903/14940 [01:04<00:16, 185.15patch/s]
80%|███████▉ | 11922/14940 [01:04<00:16, 185.28patch/s]
80%|███████▉ | 11941/14940 [01:04<00:16, 185.21patch/s]
80%|████████ | 11960/14940 [01:04<00:16, 186.05patch/s]
80%|████████ | 11979/14940 [01:04<00:15, 185.99patch/s]
80%|████████ | 11998/14940 [01:04<00:15, 185.29patch/s]
80%|████████ | 12017/14940 [01:05<00:15, 185.87patch/s]
81%|████████ | 12036/14940 [01:05<00:15, 186.22patch/s]
81%|████████ | 12055/14940 [01:05<00:15, 186.05patch/s]
81%|████████ | 12074/14940 [01:05<00:15, 185.87patch/s]
81%|████████ | 12093/14940 [01:05<00:15, 185.65patch/s]
81%|████████ | 12112/14940 [01:05<00:15, 185.69patch/s]
81%|████████ | 12131/14940 [01:05<00:15, 185.40patch/s]
81%|████████▏ | 12150/14940 [01:05<00:15, 185.27patch/s]
81%|████████▏ | 12169/14940 [01:05<00:15, 182.82patch/s]
82%|████████▏ | 12188/14940 [01:05<00:15, 181.59patch/s]
82%|████████▏ | 12207/14940 [01:06<00:15, 181.23patch/s]
82%|████████▏ | 12226/14940 [01:06<00:14, 181.76patch/s]
82%|████████▏ | 12245/14940 [01:06<00:14, 182.79patch/s]
82%|████████▏ | 12264/14940 [01:06<00:14, 184.41patch/s]
82%|████████▏ | 12283/14940 [01:06<00:14, 184.54patch/s]
82%|████████▏ | 12302/14940 [01:06<00:14, 184.18patch/s]
82%|████████▏ | 12321/14940 [01:06<00:14, 185.20patch/s]
83%|████████▎ | 12340/14940 [01:06<00:14, 185.32patch/s]
83%|████████▎ | 12359/14940 [01:06<00:13, 184.65patch/s]
83%|████████▎ | 12378/14940 [01:07<00:13, 184.34patch/s]
83%|████████▎ | 12397/14940 [01:07<00:13, 184.31patch/s]
83%|████████▎ | 12416/14940 [01:07<00:13, 184.60patch/s]
83%|████████▎ | 12435/14940 [01:07<00:13, 183.80patch/s]
83%|████████▎ | 12454/14940 [01:07<00:13, 183.20patch/s]
83%|████████▎ | 12473/14940 [01:07<00:13, 183.98patch/s]
84%|████████▎ | 12492/14940 [01:07<00:13, 184.36patch/s]
84%|████████▎ | 12511/14940 [01:07<00:13, 184.68patch/s]
84%|████████▍ | 12530/14940 [01:07<00:13, 184.86patch/s]
84%|████████▍ | 12549/14940 [01:07<00:12, 184.38patch/s]
84%|████████▍ | 12568/14940 [01:08<00:12, 183.33patch/s]
84%|████████▍ | 12587/14940 [01:08<00:12, 184.96patch/s]
84%|████████▍ | 12606/14940 [01:08<00:12, 186.31patch/s]
85%|████████▍ | 12625/14940 [01:08<00:12, 186.87patch/s]
85%|████████▍ | 12644/14940 [01:08<00:12, 187.59patch/s]
85%|████████▍ | 12663/14940 [01:08<00:12, 188.17patch/s]
85%|████████▍ | 12682/14940 [01:08<00:12, 188.16patch/s]
85%|████████▌ | 12701/14940 [01:08<00:11, 187.73patch/s]
85%|████████▌ | 12720/14940 [01:08<00:11, 187.16patch/s]
85%|████████▌ | 12739/14940 [01:08<00:11, 186.21patch/s]
85%|████████▌ | 12758/14940 [01:09<00:11, 185.37patch/s]
86%|████████▌ | 12777/14940 [01:09<00:11, 184.93patch/s]
86%|████████▌ | 12796/14940 [01:09<00:11, 184.78patch/s]
86%|████████▌ | 12815/14940 [01:09<00:11, 185.13patch/s]
86%|████████▌ | 12834/14940 [01:09<00:11, 185.12patch/s]
86%|████████▌ | 12853/14940 [01:09<00:11, 184.72patch/s]
86%|████████▌ | 12872/14940 [01:09<00:11, 184.47patch/s]
86%|████████▋ | 12891/14940 [01:09<00:11, 184.87patch/s]
86%|████████▋ | 12910/14940 [01:09<00:10, 185.03patch/s]
87%|████████▋ | 12929/14940 [01:09<00:10, 185.33patch/s]
87%|████████▋ | 12948/14940 [01:10<00:10, 185.29patch/s]
87%|████████▋ | 12967/14940 [01:10<00:10, 185.41patch/s]
87%|████████▋ | 12986/14940 [01:10<00:10, 185.54patch/s]
87%|████████▋ | 13005/14940 [01:10<00:10, 186.28patch/s]
87%|████████▋ | 13024/14940 [01:10<00:10, 186.92patch/s]
87%|████████▋ | 13043/14940 [01:10<00:10, 185.85patch/s]
87%|████████▋ | 13062/14940 [01:10<00:10, 186.55patch/s]
88%|████████▊ | 13081/14940 [01:10<00:09, 186.73patch/s]
88%|████████▊ | 13100/14940 [01:10<00:09, 187.16patch/s]
88%|████████▊ | 13119/14940 [01:10<00:09, 187.46patch/s]
88%|████████▊ | 13138/14940 [01:11<00:09, 187.66patch/s]
88%|████████▊ | 13157/14940 [01:11<00:09, 187.98patch/s]
88%|████████▊ | 13176/14940 [01:11<00:09, 188.44patch/s]
88%|████████▊ | 13195/14940 [01:11<00:09, 188.85patch/s]
88%|████████▊ | 13214/14940 [01:11<00:09, 188.24patch/s]
89%|████████▊ | 13233/14940 [01:11<00:09, 187.21patch/s]
89%|████████▊ | 13252/14940 [01:11<00:09, 185.35patch/s]
89%|████████▉ | 13271/14940 [01:11<00:09, 183.19patch/s]
89%|████████▉ | 13290/14940 [01:11<00:09, 181.03patch/s]
89%|████████▉ | 13309/14940 [01:12<00:08, 181.87patch/s]
89%|████████▉ | 13328/14940 [01:12<00:08, 182.92patch/s]
89%|████████▉ | 13348/14940 [01:12<00:08, 185.08patch/s]
89%|████████▉ | 13367/14940 [01:12<00:08, 186.03patch/s]
90%|████████▉ | 13386/14940 [01:12<00:08, 186.45patch/s]
90%|████████▉ | 13405/14940 [01:12<00:08, 186.24patch/s]
90%|████████▉ | 13424/14940 [01:12<00:08, 185.50patch/s]
90%|████████▉ | 13443/14940 [01:12<00:08, 185.02patch/s]
90%|█████████ | 13462/14940 [01:12<00:07, 185.19patch/s]
90%|█████████ | 13481/14940 [01:12<00:07, 185.98patch/s]
90%|█████████ | 13500/14940 [01:13<00:07, 187.07patch/s]
90%|█████████ | 13519/14940 [01:13<00:07, 187.92patch/s]
91%|█████████ | 13538/14940 [01:13<00:07, 187.93patch/s]
91%|█████████ | 13557/14940 [01:13<00:07, 187.21patch/s]
91%|█████████ | 13576/14940 [01:13<00:07, 184.01patch/s]
91%|█████████ | 13595/14940 [01:13<00:07, 182.15patch/s]
91%|█████████ | 13614/14940 [01:13<00:07, 182.59patch/s]
91%|█████████▏| 13633/14940 [01:13<00:07, 184.26patch/s]
91%|█████████▏| 13652/14940 [01:13<00:06, 185.65patch/s]
92%|█████████▏| 13671/14940 [01:13<00:06, 185.13patch/s]
92%|█████████▏| 13690/14940 [01:14<00:06, 184.13patch/s]
92%|█████████▏| 13709/14940 [01:14<00:06, 183.24patch/s]
92%|█████████▏| 13728/14940 [01:14<00:06, 183.85patch/s]
92%|█████████▏| 13747/14940 [01:14<00:06, 184.86patch/s]
92%|█████████▏| 13766/14940 [01:14<00:06, 186.28patch/s]
92%|█████████▏| 13785/14940 [01:14<00:06, 186.95patch/s]
92%|█████████▏| 13804/14940 [01:14<00:06, 187.46patch/s]
93%|█████████▎| 13824/14940 [01:14<00:05, 188.29patch/s]
93%|█████████▎| 13843/14940 [01:14<00:05, 188.48patch/s]
93%|█████████▎| 13862/14940 [01:14<00:05, 188.24patch/s]
93%|█████████▎| 13881/14940 [01:15<00:05, 186.00patch/s]
93%|█████████▎| 13900/14940 [01:15<00:05, 186.09patch/s]
93%|█████████▎| 13919/14940 [01:15<00:05, 186.73patch/s]
93%|█████████▎| 13938/14940 [01:15<00:05, 186.47patch/s]
93%|█████████▎| 13957/14940 [01:15<00:05, 186.56patch/s]
94%|█████████▎| 13976/14940 [01:15<00:05, 187.00patch/s]
94%|█████████▎| 13995/14940 [01:15<00:05, 187.69patch/s]
94%|█████████▍| 14014/14940 [01:15<00:04, 187.85patch/s]
94%|█████████▍| 14033/14940 [01:15<00:04, 187.79patch/s]
94%|█████████▍| 14052/14940 [01:16<00:04, 187.67patch/s]
94%|█████████▍| 14071/14940 [01:16<00:04, 187.78patch/s]
94%|█████████▍| 14091/14940 [01:16<00:04, 188.56patch/s]
94%|█████████▍| 14111/14940 [01:16<00:04, 189.03patch/s]
95%|█████████▍| 14131/14940 [01:16<00:04, 189.27patch/s]
95%|█████████▍| 14150/14940 [01:16<00:04, 188.23patch/s]
95%|█████████▍| 14169/14940 [01:16<00:04, 187.34patch/s]
95%|█████████▍| 14188/14940 [01:16<00:04, 186.90patch/s]
95%|█████████▌| 14207/14940 [01:16<00:03, 187.65patch/s]
95%|█████████▌| 14226/14940 [01:16<00:03, 187.98patch/s]
95%|█████████▌| 14245/14940 [01:17<00:03, 188.23patch/s]
95%|█████████▌| 14264/14940 [01:17<00:03, 187.65patch/s]
96%|█████████▌| 14283/14940 [01:17<00:03, 187.12patch/s]
96%|█████████▌| 14302/14940 [01:17<00:03, 186.68patch/s]
96%|█████████▌| 14321/14940 [01:17<00:03, 187.08patch/s]
96%|█████████▌| 14341/14940 [01:17<00:03, 188.03patch/s]
96%|█████████▌| 14360/14940 [01:17<00:03, 188.52patch/s]
96%|█████████▋| 14380/14940 [01:17<00:02, 188.98patch/s]
96%|█████████▋| 14400/14940 [01:17<00:02, 189.33patch/s]
97%|█████████▋| 14419/14940 [01:17<00:02, 189.53patch/s]
97%|█████████▋| 14438/14940 [01:18<00:02, 189.40patch/s]
97%|█████████▋| 14457/14940 [01:18<00:02, 189.10patch/s]
97%|█████████▋| 14476/14940 [01:18<00:02, 188.27patch/s]
97%|█████████▋| 14495/14940 [01:18<00:02, 187.91patch/s]
97%|█████████▋| 14515/14940 [01:18<00:02, 188.60patch/s]
97%|█████████▋| 14534/14940 [01:18<00:02, 188.67patch/s]
97%|█████████▋| 14553/14940 [01:18<00:02, 188.37patch/s]
98%|█████████▊| 14572/14940 [01:18<00:01, 188.37patch/s]
98%|█████████▊| 14591/14940 [01:18<00:01, 188.30patch/s]
98%|█████████▊| 14610/14940 [01:18<00:01, 188.43patch/s]
98%|█████████▊| 14629/14940 [01:19<00:01, 188.31patch/s]
98%|█████████▊| 14648/14940 [01:19<00:01, 188.43patch/s]
98%|█████████▊| 14667/14940 [01:19<00:01, 188.42patch/s]
98%|█████████▊| 14686/14940 [01:19<00:01, 188.32patch/s]
98%|█████████▊| 14705/14940 [01:19<00:01, 188.35patch/s]
99%|█████████▊| 14724/14940 [01:19<00:01, 188.75patch/s]
99%|█████████▊| 14743/14940 [01:19<00:01, 188.69patch/s]
99%|█████████▉| 14762/14940 [01:19<00:00, 188.63patch/s]
99%|█████████▉| 14781/14940 [01:19<00:00, 189.01patch/s]
99%|█████████▉| 14800/14940 [01:19<00:00, 187.87patch/s]
99%|█████████▉| 14819/14940 [01:20<00:00, 185.97patch/s]
99%|█████████▉| 14838/14940 [01:20<00:00, 186.66patch/s]
99%|█████████▉| 14857/14940 [01:20<00:00, 186.95patch/s]
100%|█████████▉| 14876/14940 [01:20<00:00, 186.65patch/s]
100%|█████████▉| 14895/14940 [01:20<00:00, 187.44patch/s]
100%|█████████▉| 14914/14940 [01:20<00:00, 187.61patch/s]
100%|█████████▉| 14933/14940 [01:20<00:00, 185.62patch/s]
100%|██████████| 14940/14940 [01:20<00:00, 185.03patch/s]
<mne.viz._brain._brain.Brain object at 0x7f3787ce7ad0>
Plot the RSA timecourse at the peak vertex
plt.figure()
plt.plot(rsa_vals.times, rsa_vals.data[peak_vertex])
plt.xlabel("Time (s)")
plt.ylabel("Kendall-Tau (alpha)")
plt.title(f"RSA values at vert {peak_vertex}")
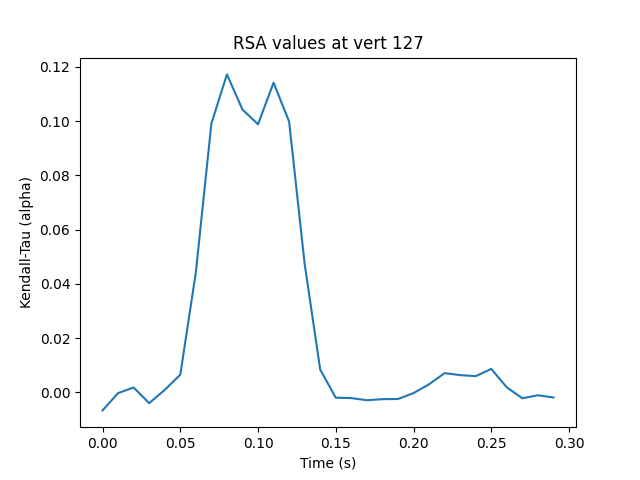
Text(0.5, 1.0, 'RSA values at vert 127')
Total running time of the script: (1 minutes 32.705 seconds)