Note
Go to the end to download the full example code. or to run this example in your browser via Binder
Mayer Wave Parametrisation#
Mayer waves are spontaneous oscillations in arterial blood pressure with a frequency of ~0.1 Hz (Ghali and Ghali, 2020; Julien, 2006; Yucel, 2016). Mayer waves are not easily removed from hemodynamic signatures of brain activity as they tend to occur on a time course often confounded with the frequency of a sensory task, for example, and/or the cortical hemodynamic response to that task.
This example demonstrates how to use the Fitting Oscillations & One Over F (FOOOF) [1] method to quanitfy Mayer wave parameters in fNIRS data. This is based on the description provided in [2].
This tutorial is heavily based on the tutorials provided by the FOOOF authors over at https://fooof-tools.github.io/fooof. You should read their excellent documentation. Their work should be considered the primary resource, and this is just an example of how to apply it to fNIRS data for the purpose of extracting Mayer waves oscillation parameters.
# Authors: Robert Luke <mail@robertluke.net>
#
# License: BSD (3-clause)
import os
import matplotlib.pyplot as plt
import mne
import numpy as np
from fooof import FOOOF
from mne.preprocessing.nirs import beer_lambert_law, optical_density
from mne_nirs.channels import get_long_channels
from mne_nirs.preprocessing import quantify_mayer_fooof
/home/circleci/project/examples/general/plot_40_mayer.py:47: DeprecationWarning:
The `fooof` package is being deprecated and replaced by the `specparam` (spectral parameterization) package.
This version of `fooof` (1.1) is fully functional, but will not be further updated.
New projects are recommended to update to using `specparam` (see Changelog for details).
from fooof import FOOOF
Import and preprocess data#
We read in the data and convert to haemoglobin concentration.
fnirs_data_folder = mne.datasets.fnirs_motor.data_path()
fnirs_raw_dir = os.path.join(fnirs_data_folder, "Participant-1")
raw = mne.io.read_raw_nirx(fnirs_raw_dir, verbose=True).load_data()
raw = optical_density(raw)
raw.resample(2)
raw = beer_lambert_law(raw, ppf=0.1)
raw = raw.pick(picks="hbo")
raw = get_long_channels(raw, min_dist=0.025, max_dist=0.045)
raw
Loading /home/circleci/mne_data/MNE-fNIRS-motor-data/Participant-1
Process data with FOOOF#
Next we estimate the power spectral density of the data and pass this to the FOOOF algorithm.
I recommend using the FOOOF algorithm as provided by the authors rather than reimplementation or custom plotting etc. Their code is of excellent quality, well maintained, thoroughly documented, and they have considered many edge cases.
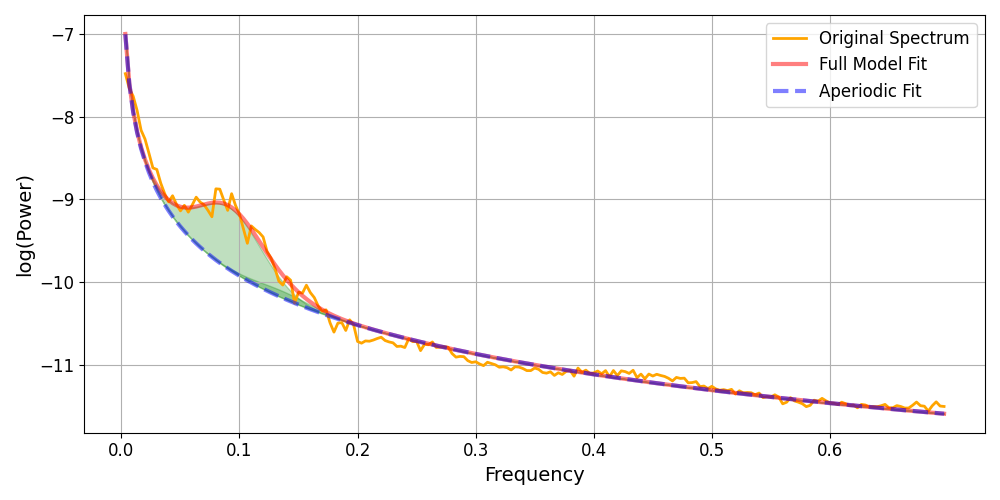
Below we plot the spectrum of the data, the FOOOF fit of oscillations, and aperiodic component. Note the bump at 0.1 Hz that reflects the Mayer wave activity.
Note that the activity is not a perfect peak at 0.1 Hz, but is spread across neighbouring frequencies. Additionally, the peak does not occur at exactly 0.1 Hz, but instead seems to peak at approximately 0.09 Hz. The shaded area illustrates the oscillation fitted by the FOOOF algorithm, it matches well to the data.
def scale_up_spectra(spectra, freqs):
"""
FOOOF requires the frequency values to be higher than the fNIRS data
permits, so we scale the values up by 10 here, and then will scale
the frequency values down by 10 later.
"""
freqs = freqs * 10
return spectra, freqs
# Prepare data for FOOOF
psd = raw.compute_psd(fmin=0.001, fmax=1.0, tmin=0, tmax=None, n_overlap=300, n_fft=600)
spectra, freqs = psd.get_data(return_freqs=True)
spectra, freqs = scale_up_spectra(spectra, freqs)
# Specify the model, note that frequency values here are times 10
fm = FOOOF(peak_width_limits=(0.5, 12.0))
# Set the frequency range to fit the model, again these are times 10
freq_range = [0.001, 7]
fm.fit(freqs, np.mean(spectra, axis=0), freq_range)
fig, axs = plt.subplots(1, 1, figsize=(10, 5))
fm.plot(plot_peaks="shade", data_kwargs={"color": "orange"}, ax=axs)
# Correct for x10 scaling above
plt.xticks([0, 1, 2, 3, 4, 5, 6], [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6])
([<matplotlib.axis.XTick object at 0x7ff02d026b60>, <matplotlib.axis.XTick object at 0x7ff02d027220>, <matplotlib.axis.XTick object at 0x7fefbc2b55d0>, <matplotlib.axis.XTick object at 0x7fefbc2b78e0>, <matplotlib.axis.XTick object at 0x7fefbc2b7190>, <matplotlib.axis.XTick object at 0x7fefbc2b5f30>, <matplotlib.axis.XTick object at 0x7fefe9fe5ae0>], [Text(0, 0, '0.0'), Text(1, 0, '0.1'), Text(2, 0, '0.2'), Text(3, 0, '0.3'), Text(4, 0, '0.4'), Text(5, 0, '0.5'), Text(6, 0, '0.6')])
Use MNE-NIRS to quantify Mayer wave oscillation#
MNE-NIRS provides a convenient function to estimate the Mayer wave parameters that takes care of the frequency scaling and selects the component most likely associated with the Mayer wave. It returns this data in a pandas dataframe for your convenience. It uses the FOOOF algorithm under the hood, so ensure you cite the original authors if you use this function.
quantify_mayer_fooof(raw.pick("hbo"), extra_df_fields={"Study": "Online tutorial"})
Conclusion#
We have demonstrated how to use the FOOOF algorithm for quantifying Mayer wave parameters, and highlighted the quantify_mayer_fooof for conveniently applying this analysis to fNIRS data with MNE-NIRS.
An example measurement illustrated what the presence of a Mayer wave looks like with a power spectral density. The measurement also illustrated that the Mayer wave is not a perfect sinusoid, as evidenced by the broad spectral content. Further, the example illustrated that the Mayer wave is not always precisely locked to 0.1 Hz, both visual inspection and FOOOF quantification indicate a 0.09 Hz centre frequency.
See the article Luke (2021) [2] for further details on this analysis approach, and normative data from over 300 fNIRS measurements. This article also demonstrates that using short-channel systemic component correction algorithms can reduce the Mayer wave component in the signal (see also Yucel 2016). See both the GLM tutorial and signal enhancement tutorial for how to use short channels in either a GLM or averaging analysis with MNE-NIRS.
Bibliography#
Total running time of the script: (0 minutes 3.598 seconds)
Estimated memory usage: 462 MB
