mne.time_frequency.tfr_morlet#
- mne.time_frequency.tfr_morlet(inst, freqs, n_cycles, use_fft=False, return_itc=True, decim=1, n_jobs=None, picks=None, zero_mean=True, average=True, output='power', verbose=None)[source]#
Compute Time-Frequency Representation (TFR) using Morlet wavelets.
Same computation as
tfr_array_morlet, but operates onEpochsorEvokedobjects instead ofNumPy arrays.- Parameters:
- inst
Epochs|Evoked The epochs or evoked object.
- freqs
arrayoffloat, shape (n_freqs,) The frequencies of interest in Hz.
- n_cycles
int|arrayofint, shape (n_freqs,) Number of cycles in the wavelet, either a fixed number or one per frequency. The number of cycles
n_cyclesand the frequencies of interestfreqsdefine the temporal window length. See notes for additional information about the relationship between those arguments and about time and frequency smoothing.- use_fft
bool, defaultFalse The fft based convolution or not.
- return_itc
bool, defaultTrue Return inter-trial coherence (ITC) as well as averaged power. Must be
Falsefor evoked data.- decim
int|slice, default 1 To reduce memory usage, decimation factor after time-frequency decomposition.
Note
Decimation is done after convolutions and may create aliasing artifacts.
- n_jobs
int|None The number of jobs to run in parallel. If
-1, it is set to the number of CPU cores. Requires thejoblibpackage.None(default) is a marker for ‘unset’ that will be interpreted asn_jobs=1(sequential execution) unless the call is performed under ajoblib.parallel_backend()context manager that sets another value forn_jobs.- picksarray_like of
int|None, defaultNone The indices of the channels to decompose. If None, all available good data channels are decomposed.
- zero_mean
bool, defaultTrue Make sure the wavelet has a mean of zero.
New in version 0.13.0.
- average
bool, defaultTrue If
Falsereturn anEpochsTFRcontaining separate TFRs for each epoch. IfTruereturn anAverageTFRcontaining the average of all TFRs across epochs.Note
Using
average=Trueis functionally equivalent to usingaverage=Falsefollowed byEpochsTFR.average(), but is more memory efficient.New in version 0.13.0.
- output
str Can be
"power"(default) or"complex". If"complex", thenaveragemust beFalse.New in version 0.15.0.
- verbose
bool|str|int|None Control verbosity of the logging output. If
None, use the default verbosity level. See the logging documentation andmne.verbose()for details. Should only be passed as a keyword argument.
- inst
- Returns:
- power
AverageTFR|EpochsTFR The averaged or single-trial power.
- itc
AverageTFR|EpochsTFR The inter-trial coherence (ITC). Only returned if return_itc is True.
- power
See also
Notes
The Morlet wavelets follow the formulation in [1].
In spectrotemporal analysis (as with traditional fourier methods), the temporal and spectral resolution are interrelated: longer temporal windows allow more precise frequency estimates; shorter temporal windows “smear” frequency estimates while providing more precise timing information.
Time-frequency representations are computed using a sliding temporal window. Either the temporal window has a fixed length independent of frequency, or the temporal window decreases in length with increased frequency.
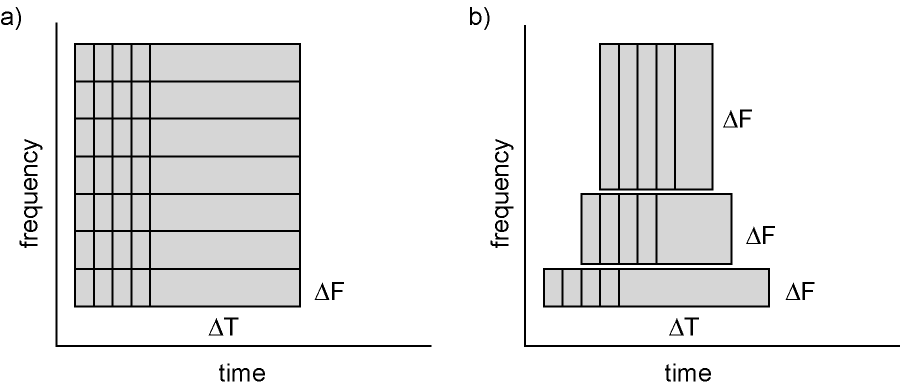
Figure: Time and frequency smoothing. (a) For a fixed length temporal window the time and frequency smoothing remains fixed. (b) For temporal windows that decrease with frequency, the temporal smoothing decreases and the frequency smoothing increases with frequency. Source: FieldTrip tutorial: Time-frequency analysis using Hanning window, multitapers and wavelets.
In MNE-Python, the temporal window length is defined by the arguments
freqsandn_cycles, respectively defining the frequencies of interest and the number of cycles: \(T = \frac{\mathtt{n\_cycles}}{\mathtt{freqs}}\)A fixed number of cycles for all frequencies will yield a temporal window which decreases with frequency. For example,
freqs=np.arange(1, 6, 2)andn_cycles=2yieldsT=array([2., 0.7, 0.4]).To use a temporal window with fixed length, the number of cycles has to be defined based on the frequency. For example,
freqs=np.arange(1, 6, 2)andn_cycles=freqs / 2yieldsT=array([0.5, 0.5, 0.5]).In wavelet analysis, the oscillation that is defined by
n_cyclesis tapered by a Gaussian taper, i.e., the edges of the wavelet are dampened. This means that reporting the number of cycles is not necessarily helpful for understanding the amount of temporal smoothing that has been applied (see [2]). Instead, the full width at half-maximum (FWHM) of the wavelet can be reported.The FWHM of the wavelet at a specific frequency is defined as: \(\mathrm{FWHM} = \frac{\mathtt{n\_cycles} \times \sqrt{2 \ln{2}}}{\pi \times \mathtt{freq}}\) (cf. eq. 4 in [2]).
See
mne.time_frequency.morlet()for more information about the Morlet wavelet.References
Examples using mne.time_frequency.tfr_morlet#
Non-parametric 1 sample cluster statistic on single trial power
Non-parametric between conditions cluster statistic on single trial power

Mass-univariate twoway repeated measures ANOVA on single trial power

Spatiotemporal permutation F-test on full sensor data
Time-frequency on simulated data (Multitaper vs. Morlet vs. Stockwell vs. Hilbert)
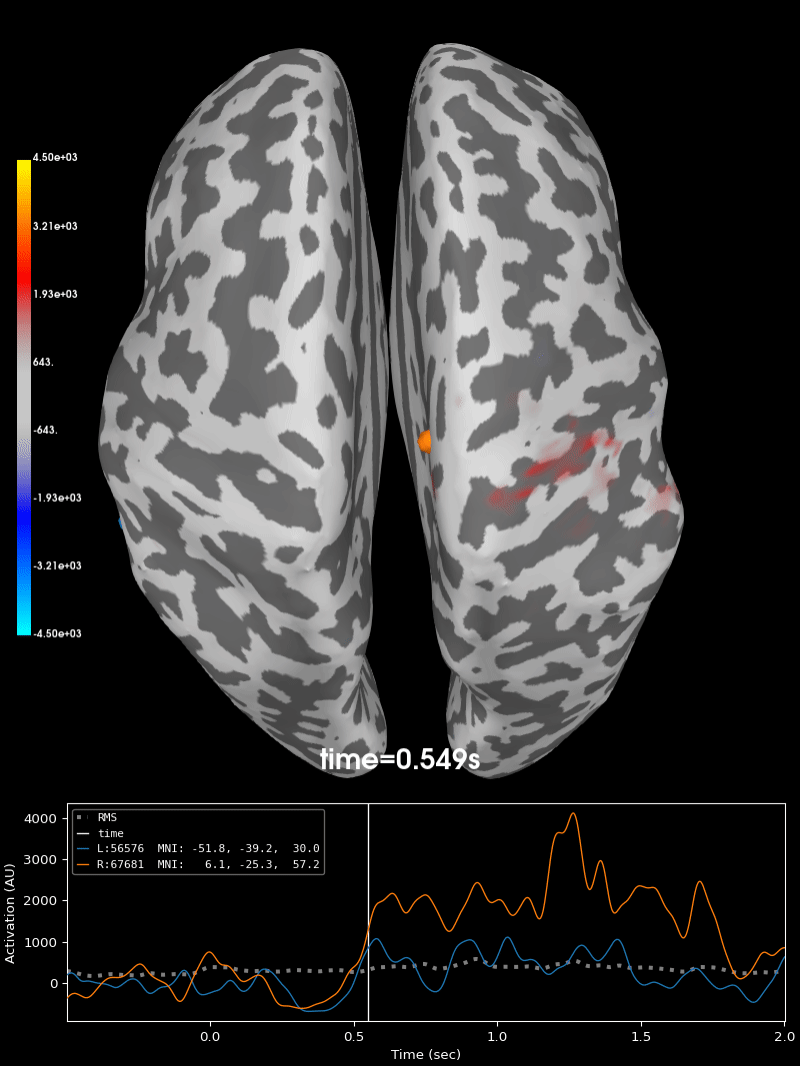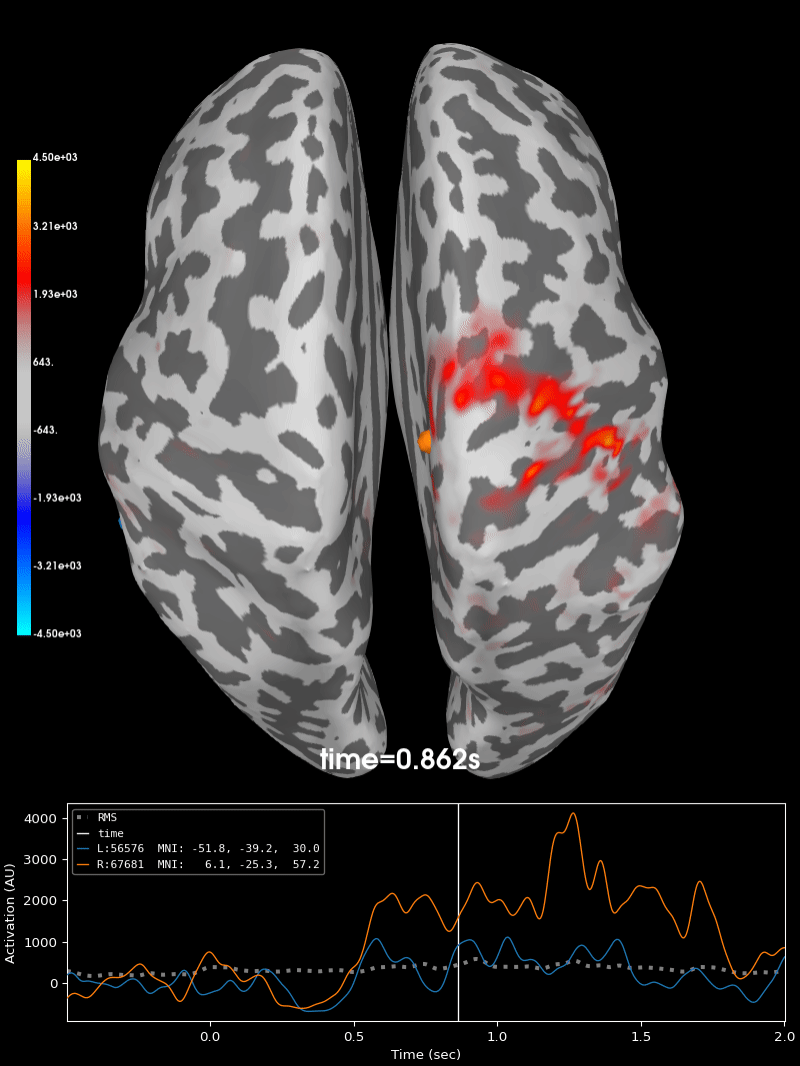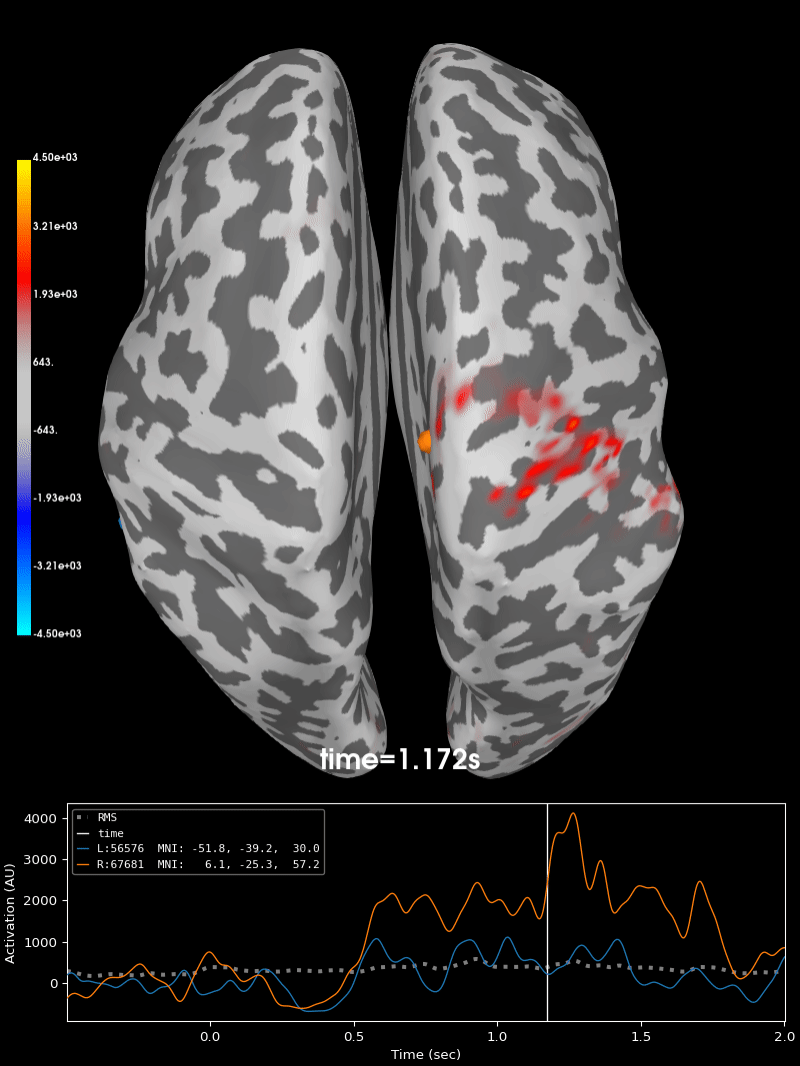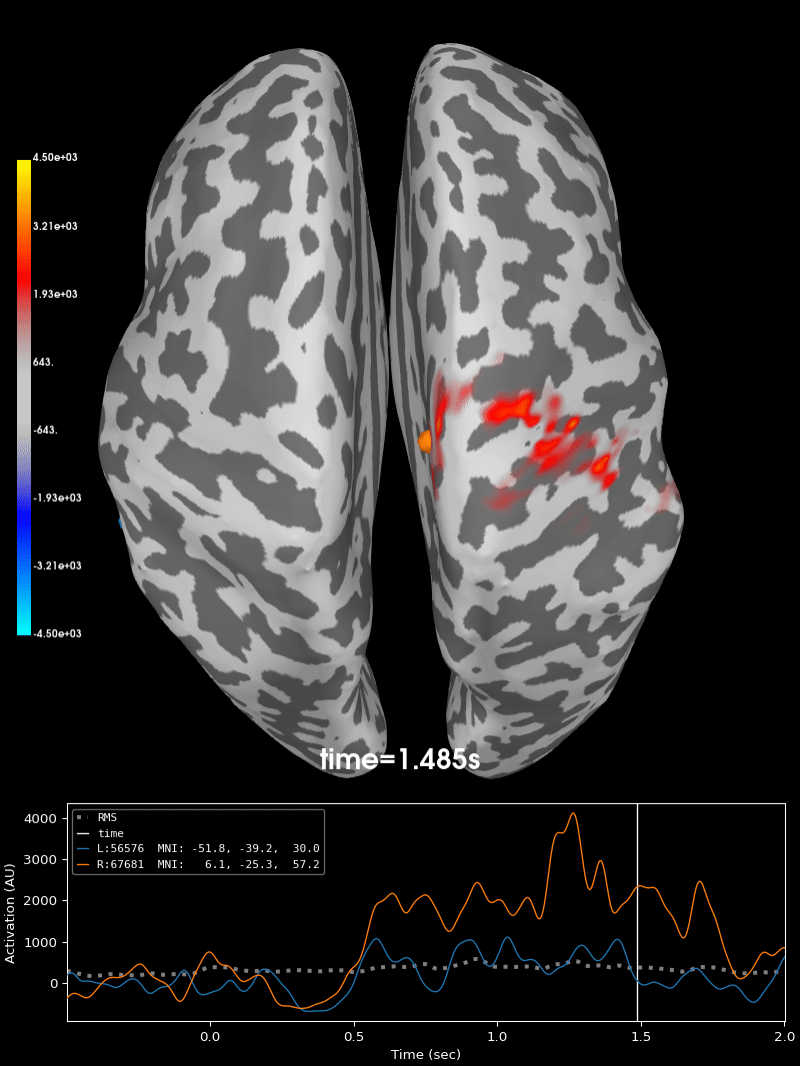
Compute source level time-frequency timecourses using a DICS beamformer