mne.time_frequency.morlet

mne.time_frequency.morlet(sfreq, freqs, n_cycles=7.0, sigma=None, zero_mean=False)

Compute Morlet wavelets for the given frequency range.

Parameters:

sfreqfloat

The sampling Frequency.

freqsfloat | array_like, shape (n_freqs,)

Frequencies to compute Morlet wavelets for.

n_cyclesfloat | array_like, shape (n_freqs,)

Number of cycles. Can be a fixed number (float) or one per frequency (array-like).

sigmafloat, default None

It controls the width of the wavelet ie its temporal resolution. If sigma is None the temporal resolution is adapted with the frequency like for all wavelet transform. The higher the frequency the shorter is the wavelet. If sigma is fixed the temporal resolution is fixed like for the short time Fourier transform and the number of oscillations increases with the frequency.

zero_meanbool, default False

Make sure the wavelet has a mean of zero.

Returns:

Wslist of ndarray | ndarray

The wavelets time series. If freqs was a float, a single ndarray is returned instead of a list of ndarray.

See also

mne.time_frequency.fwhm

Notes

The Morlet wavelets follow the formulation in Tallon-Baudry et al.[1].

Convolution of a signal with a Morlet wavelet will impose temporal smoothing that is determined by the duration of the wavelet. In MNE-Python, the duration of the wavelet is determined by the sigma parameter, which gives the standard deviation of the wavelet’s Gaussian envelope (our wavelets extend to ±5 standard deviations to ensure values very close to zero at the endpoints). Some authors (e.g., Cohen[2]) recommend specifying and reporting wavelet duration in terms of the full-width half-maximum (FWHM) of the wavelet’s Gaussian envelope. The FWHM is related to sigma by the following identity: \(\mathrm{FWHM} = \sigma \times 2 \sqrt{2 \ln{2}}\) (or the equivalent in Python code: fwhm = sigma * 2 * np.sqrt(2 * np.log(2))). If sigma is not provided, it is computed from n_cycles as \(\frac{\mathtt{n\_cycles}}{2 \pi f}\) where \(f\) is the frequency of the wavelet oscillation (given by freqs). Thus when sigma=None the FWHM will be given by

\[\mathrm{FWHM} = \frac{\mathtt{n\_cycles} \times \sqrt{2 \ln{2}}}{\pi \times f}\]

(cf. eq. 4 in [2]). To create wavelets with a chosen FWHM, one can compute:

n_cycles = desired_fwhm * np.pi * np.array(freqs) / np.sqrt(2 * np.log(2))

to get an array of values for n_cycles that yield the desired FWHM at each frequency in freqs. If you want different FWHM values at each frequency, do the same computation with desired_fwhm as an array of the same shape as freqs.

References

[1]

Catherine Tallon-Baudry, Olivier Bertrand, Claude Delpuech, and Jacques Pernier. Oscillatory Gamma-Band (30–70 Hz) Activity Induced by a Visual Search Task in Humans. Journal of Neuroscience, pages 722–734, 1997. doi:10.1523/JNEUROSCI.17-02-00722.1997.

[2] (1,2)

Michael X Cohen. A better way to define and describe Morlet wavelets for time-frequency analysis. NeuroImage, 199:81–86, 2019. doi:10.1016/j.neuroimage.2019.05.048.

Examples

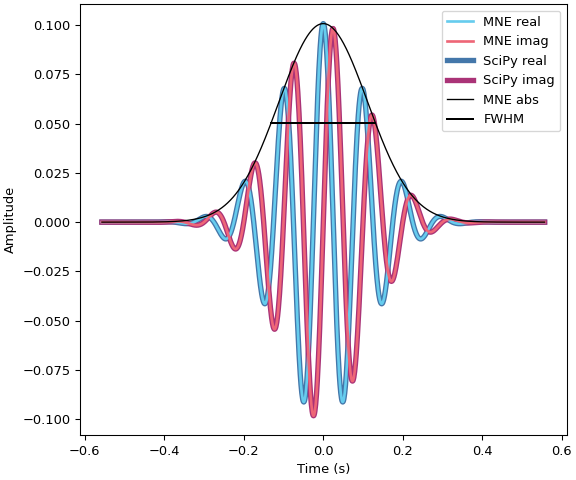
Let’s show a simple example of the relationship between n_cycles and the FWHM using mne.time_frequency.fwhm(), as well as the equivalent call using scipy.signal.morlet2():

import numpy as np
from scipy.signal import morlet2 as sp_morlet
import matplotlib.pyplot as plt
from mne.time_frequency import morlet, fwhm

sfreq, freq, n_cycles = 1000., 10, 7  # i.e., 700 ms
this_fwhm = fwhm(freq, n_cycles)
wavelet = morlet(sfreq=sfreq, freqs=freq, n_cycles=n_cycles)
M, w = len(wavelet), n_cycles # convert to SciPy convention
s = w * sfreq / (2 * freq * np.pi)  # from SciPy docs
wavelet_sp = sp_morlet(M, s, w) * np.sqrt(2)  # match our normalization

_, ax = plt.subplots(layout="constrained")
colors = {
    ('MNE', 'real'): '#66CCEE',
    ('SciPy', 'real'): '#4477AA',
    ('MNE', 'imag'): '#EE6677',
    ('SciPy', 'imag'): '#AA3377',
}
lw = dict(MNE=2, SciPy=4)
zorder = dict(MNE=5, SciPy=4)
t = np.arange(-M // 2 + 1, M // 2 + 1) / sfreq
for name, w in (('MNE', wavelet), ('SciPy', wavelet_sp)):
    for kind in ('real', 'imag'):
        ax.plot(t, getattr(w, kind), label=f'{name} {kind}',
                lw=lw[name], color=colors[(name, kind)],
                zorder=zorder[name])
ax.plot(t, np.abs(wavelet), label=f'MNE abs', color='k', lw=1., zorder=6)
half_max = np.max(np.abs(wavelet)) / 2.
ax.plot([-this_fwhm / 2., this_fwhm / 2.], [half_max, half_max],
        color='k', linestyle='-', label='FWHM', zorder=6)
ax.legend(loc='upper right')
ax.set(xlabel='Time (s)', ylabel='Amplitude')

Examples using mne.time_frequency.morlet

Background information on filtering

Background information on filtering