mne.time_frequency.tfr_array_multitaper#

mne.time_frequency.tfr_array_multitaper(epoch_data, sfreq, freqs, n_cycles=7.0, zero_mean=True, time_bandwidth=4.0, use_fft=True, decim=1, output='complex', n_jobs=None, *, verbose=None)[source]#

Compute Time-Frequency Representation (TFR) using DPSS tapers.

Same computation as tfr_multitaper, but operates on NumPy arrays instead of Epochs or Evoked objects.

Parameters:

epoch_dataarray of shape (n_epochs, n_channels, n_times)

The epochs.

sfreqfloat

Sampling frequency of the data in Hz.

freqsarray of float, shape (n_freqs,)

The frequencies of interest in Hz.

n_cyclesint | array of int, shape (n_freqs,)

Number of cycles in the wavelet, either a fixed number or one per frequency. The number of cycles n_cycles and the frequencies of interest freqs define the temporal window length. See notes for additional information about the relationship between those arguments and about time and frequency smoothing.

zero_meanbool

If True, make sure the wavelets have a mean of zero. Defaults to True.

time_bandwidthfloat ≥ 2.0

Product between the temporal window length (in seconds) and the full frequency bandwidth (in Hz). This product can be seen as the surface of the window on the time/frequency plane and controls the frequency bandwidth (thus the frequency resolution) and the number of good tapers. See notes for additional information.

use_fftbool

Use the FFT for convolutions or not. Defaults to True.

decimint | slice, default 1

To reduce memory usage, decimation factor after time-frequency decomposition.

if int, returns tfr[..., ::decim].
if slice, returns tfr[..., decim].

Note

Decimation is done after convolutions and may create aliasing artifacts.

outputstr, default ‘complex’

'complex' : single trial per taper complex values.
'power' : single trial power.
'phase' : single trial per taper phase.
'avg_power' : average of single trial power.
'itc' : inter-trial coherence.
'avg_power_itc' : average of single trial power and inter-trial coherence across trials.

n_jobsint | None

The number of jobs to run in parallel. If -1, it is set to the number of CPU cores. Requires the joblib package. None (default) is a marker for ‘unset’ that will be interpreted as n_jobs=1 (sequential execution) unless the call is performed under a joblib.parallel_config context manager that sets another value for n_jobs.

verbosebool | str | int | None

Control verbosity of the logging output. If None, use the default verbosity level. See the logging documentation and mne.verbose() for details. Should only be passed as a keyword argument.

Returns:

outarray

Time frequency transform of epoch_data.

if output in ('complex',' 'phase'), array of shape (n_epochs, n_chans, n_tapers, n_freqs, n_times)
if output is 'power', array of shape (n_epochs, n_chans, n_freqs, n_times)
else, array of shape (n_chans, n_freqs, n_times)

If output is 'avg_power_itc', the real values in out contain the average power and the imaginary values contain the inter-trial coherence: \(out = power_{avg} + i * ITC\).

See also

mne.time_frequency.tfr_multitaper
mne.time_frequency.tfr_morlet
mne.time_frequency.tfr_array_morlet
mne.time_frequency.tfr_stockwell
mne.time_frequency.tfr_array_stockwell

Notes

In spectrotemporal analysis (as with traditional fourier methods), the temporal and spectral resolution are interrelated: longer temporal windows allow more precise frequency estimates; shorter temporal windows “smear” frequency estimates while providing more precise timing information.

Time-frequency representations are computed using a sliding temporal window. Either the temporal window has a fixed length independent of frequency, or the temporal window decreases in length with increased frequency.

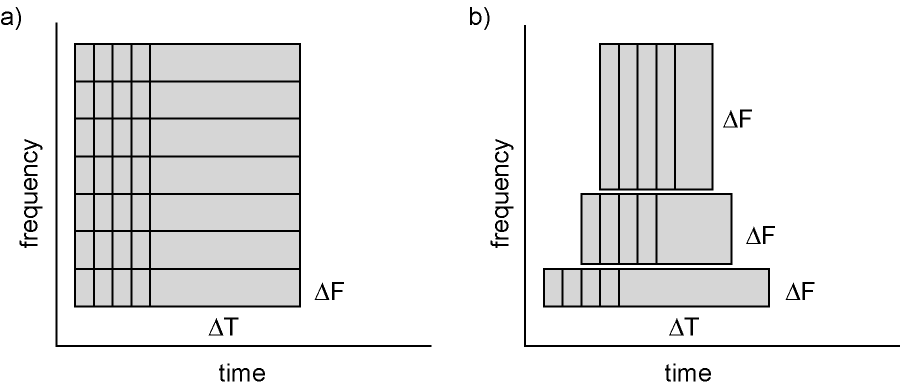
https://www.fieldtriptoolbox.org/assets/img/tutorial/timefrequencyanalysis/figure1.png

Figure: Time and frequency smoothing. (a) For a fixed length temporal window the time and frequency smoothing remains fixed. (b) For temporal windows that decrease with frequency, the temporal smoothing decreases and the frequency smoothing increases with frequency. Source: FieldTrip tutorial: Time-frequency analysis using Hanning window, multitapers and wavelets.

In MNE-Python, the multitaper temporal window length is defined by the arguments freqs and n_cycles, respectively defining the frequencies of interest and the number of cycles: \(T = \frac{\mathtt{n\_cycles}}{\mathtt{freqs}}\)

A fixed number of cycles for all frequencies will yield a temporal window which decreases with frequency. For example, freqs=np.arange(1, 6, 2) and n_cycles=2 yields T=array([2., 0.7, 0.4]).

To use a temporal window with fixed length, the number of cycles has to be defined based on the frequency. For example, freqs=np.arange(1, 6, 2) and n_cycles=freqs / 2 yields T=array([0.5, 0.5, 0.5]).

In MNE-Python’s multitaper functions, the frequency bandwidth is additionally affected by the parameter time_bandwidth. The n_cycles parameter determines the temporal window length based on the frequencies of interest: \(T = \frac{\mathtt{n\_cycles}}{\mathtt{freqs}}\). The time_bandwidth parameter defines the “time-bandwidth product”, which is the product of the temporal window length (in seconds) and the frequency bandwidth (in Hz). Thus once n_cycles has been set, frequency bandwidth is determined by \(\frac{\mathrm{time~bandwidth}}{\mathrm{time~window}}\), and thus passing a larger time_bandwidth value will increase the frequency bandwidth (thereby decreasing the frequency resolution).

The increased frequency bandwidth is reached by averaging spectral estimates obtained from multiple tapers. Thus, time_bandwidth also determines the number of tapers used. MNE-Python uses only “good” tapers (tapers with minimal leakage from far-away frequencies); the number of good tapers is floor(time_bandwidth - 1). This means there is another trade-off at play, between frequency resolution and the variance reduction that multitaper analysis provides. Striving for finer frequency resolution (by setting time_bandwidth low) means fewer tapers will be used, which undermines what is unique about multitaper methods — namely their ability to improve accuracy / reduce noise in the power estimates by using several (orthogonal) tapers.

Warning

In tfr_array_multitaper and tfr_multitaper, time_bandwidth defines the product of the temporal window length with the full frequency bandwidth For example, a full bandwidth of 4 Hz at a frequency of interest of 10 Hz will “smear” the frequency estimate between 8 Hz and 12 Hz.

This is not the case for psd_array_multitaper where the argument bandwidth defines the half frequency bandwidth. In the example above, the half-frequency bandwidth is 2 Hz.

New in v0.14.0.