mne.time_frequency.tfr_array_morlet

mne.time_frequency.tfr_array_morlet(epoch_data, sfreq, freqs, n_cycles=7.0, zero_mean=False, use_fft=True, decim=1, output='complex', n_jobs=None, verbose=None)

Compute Time-Frequency Representation (TFR) using Morlet wavelets.

Same computation as tfr_morlet, but operates on NumPy arrays instead of Epochs objects.

Parameters:

epoch_dataarray of shape (n_epochs, n_channels, n_times)

The epochs.

sfreqfloat | int

Sampling frequency of the data.

freqsarray of float, shape (n_freqs,)

The frequencies of interest in Hz.

n_cyclesint | array of int, shape (n_freqs,)

Number of cycles in the wavelet, either a fixed number or one per frequency. The number of cycles n_cycles and the frequencies of interest freqs define the temporal window length. See notes for additional information about the relationship between those arguments and about time and frequency smoothing.

zero_meanbool

If True, make sure the wavelets have a mean of zero. default False.

use_fftbool

Use the FFT for convolutions or not. default True.

decimint | slice, default 1

To reduce memory usage, decimation factor after time-frequency decomposition.

• if int, returns tfr[..., ::decim].

• if slice, returns tfr[..., decim].

Note

Decimation is done after convolutions and may create aliasing artifacts.

outputstr, default 'complex'

• 'complex' : single trial complex.

• 'power' : single trial power.

• 'phase' : single trial phase.

• 'avg_power' : average of single trial power.

• 'itc' : inter-trial coherence.

• 'avg_power_itc' : average of single trial power and inter-trial coherence across trials.

n_jobsint | None

The number of jobs to run in parallel. If -1, it is set to the number of CPU cores. Requires the joblib package. None (default) is a marker for ‘unset’ that will be interpreted as n_jobs=1 (sequential execution) unless the call is performed under a joblib.parallel_config context manager that sets another value for n_jobs. The number of epochs to process at the same time. The parallelization is implemented across channels. Default 1.

verbosebool | str | int | None

Control verbosity of the logging output. If None, use the default verbosity level. See the logging documentation and mne.verbose() for details. Should only be passed as a keyword argument.

Returns:

outarray

Time frequency transform of epoch_data.

• if output in ('complex', 'phase', 'power'), array of shape (n_epochs, n_chans, n_freqs, n_times)

• else, array of shape (n_chans, n_freqs, n_times)

If output is 'avg_power_itc', the real values in out contain the average power and the imaginary values contain the ITC: \(out = power_{avg} + i * itc\).

See also

mne.time_frequency.tfr_morlet

mne.time_frequency.tfr_multitaper

mne.time_frequency.tfr_array_multitaper

mne.time_frequency.tfr_stockwell

mne.time_frequency.tfr_array_stockwell

Notes

The Morlet wavelets follow the formulation in Tallon-Baudry et al.[1].

In spectrotemporal analysis (as with traditional fourier methods), the temporal and spectral resolution are interrelated: longer temporal windows allow more precise frequency estimates; shorter temporal windows “smear” frequency estimates while providing more precise timing information.

Time-frequency representations are computed using a sliding temporal window. Either the temporal window has a fixed length independent of frequency, or the temporal window decreases in length with increased frequency.

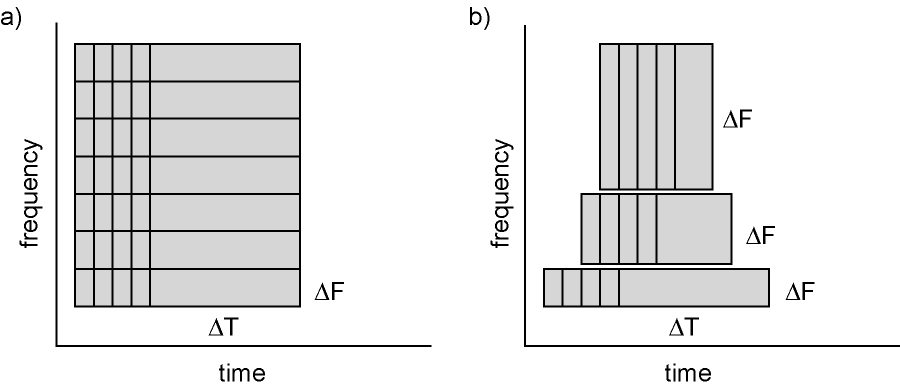
Figure: Time and frequency smoothing. (a) For a fixed length temporal window the time and frequency smoothing remains fixed. (b) For temporal windows that decrease with frequency, the temporal smoothing decreases and the frequency smoothing increases with frequency. Source: FieldTrip tutorial: Time-frequency analysis using Hanning window, multitapers and wavelets.

In MNE-Python, the length of the Morlet wavelet is affected by the arguments freqs and n_cycles, which define the frequencies of interest and the number of cycles, respectively. For the time-frequency representation, the length of the wavelet is defined such that both tails of the wavelet extend five standard deviations from the midpoint of its Gaussian envelope and that there is a sample at time zero.

The length of the wavelet is thus \(10\times\mathtt{sfreq}\cdot\sigma-1\), which is equal to \(\frac{5}{\pi} \cdot \frac{\mathtt{n\_cycles} \cdot \mathtt{sfreq}}{\mathtt{freqs}} - 1\), where \(\sigma = \frac{\mathtt{n\_cycles}}{2\pi f}\) corresponds to the standard deviation of the wavelet’s Gaussian envelope. Note that the length of the wavelet must not exceed the length of your signal.

For more information on the Morlet wavelet, see mne.time_frequency.morlet().

New in v0.14.0.

References

[1]

Catherine Tallon-Baudry, Olivier Bertrand, Claude Delpuech, and Jacques Pernier. Oscillatory Gamma-Band (30–70 Hz) Activity Induced by a Visual Search Task in Humans. Journal of Neuroscience, pages 722–734, 1997. doi:10.1523/JNEUROSCI.17-02-00722.1997.

Examples using mne.time_frequency.tfr_array_morlet

Time-frequency on simulated data (Multitaper vs. Morlet vs. Stockwell vs. Hilbert)

Time-frequency on simulated data (Multitaper vs. Morlet vs. Stockwell vs. Hilbert)