Source localization with MNE, dSPM, sLORETA, and eLORETA

The aim of this tutorial is to teach you how to compute and apply a linear minimum-norm inverse method on evoked/raw/epochs data.

import numpy as np
import matplotlib.pyplot as plt

import mne
from mne.datasets import sample
from mne.minimum_norm import make_inverse_operator, apply_inverse

Process MEG data

data_path = sample.data_path()
raw_fname = data_path / "MEG" / "sample" / "sample_audvis_filt-0-40_raw.fif"

raw = mne.io.read_raw_fif(raw_fname)  # already has an average reference
events = mne.find_events(raw, stim_channel="STI 014")

event_id = dict(aud_l=1)  # event trigger and conditions
tmin = -0.2  # start of each epoch (200ms before the trigger)
tmax = 0.5  # end of each epoch (500ms after the trigger)
raw.info["bads"] = ["MEG 2443", "EEG 053"]
baseline = (None, 0)  # means from the first instant to t = 0
reject = dict(grad=4000e-13, mag=4e-12, eog=150e-6)

epochs = mne.Epochs(
    raw,
    events,
    event_id,
    tmin,
    tmax,
    proj=True,
    picks=("meg", "eog"),
    baseline=baseline,
    reject=reject,
)

Opening raw data file /home/circleci/mne_data/MNE-sample-data/MEG/sample/sample_audvis_filt-0-40_raw.fif...
    Read a total of 4 projection items:
        PCA-v1 (1 x 102)  idle
        PCA-v2 (1 x 102)  idle
        PCA-v3 (1 x 102)  idle
        Average EEG reference (1 x 60)  idle
    Range : 6450 ... 48149 =     42.956 ...   320.665 secs
Ready.
319 events found
Event IDs: [ 1  2  3  4  5 32]
Not setting metadata
72 matching events found
Setting baseline interval to [-0.19979521315838786, 0.0] s
Applying baseline correction (mode: mean)
Created an SSP operator (subspace dimension = 3)
4 projection items activated

Compute regularized noise covariance

For more details see Computing a covariance matrix.

noise_cov = mne.compute_covariance(
    epochs, tmax=0.0, method=["shrunk", "empirical"], rank=None, verbose=True
)

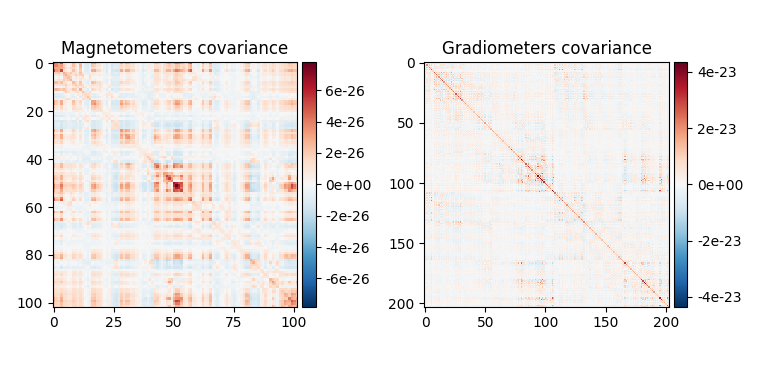
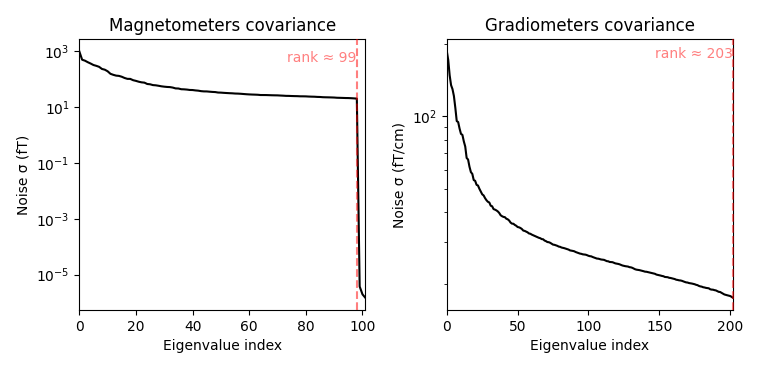
fig_cov, fig_spectra = mne.viz.plot_cov(noise_cov, raw.info)

• 
• 

Loading data for 72 events and 106 original time points ...
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on MAG : ['MEG 1711']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
    Rejecting  epoch based on EOG : ['EOG 061']
17 bad epochs dropped
Computing rank from data with rank=None
    Using tolerance 2.8e-09 (2.2e-16 eps * 305 dim * 4.2e+04  max singular value)
    Estimated rank (mag + grad): 302
    MEG: rank 302 computed from 305 data channels with 3 projectors
    Created an SSP operator (subspace dimension = 3)
    Setting small MEG eigenvalues to zero (without PCA)
Reducing data rank from 305 -> 302
Estimating covariance using SHRUNK
Done.
Estimating covariance using EMPIRICAL
Done.
Using cross-validation to select the best estimator.
Number of samples used : 1705
log-likelihood on unseen data (descending order):
   shrunk: -1468.506
   empirical: -1574.608
selecting best estimator: shrunk
[done]
Computing rank from covariance with rank=None
    Using tolerance 2.2e-14 (2.2e-16 eps * 102 dim * 0.98  max singular value)
    Estimated rank (mag): 99
    MAG: rank 99 computed from 102 data channels with 0 projectors
Computing rank from covariance with rank=None
    Using tolerance 1.6e-13 (2.2e-16 eps * 203 dim * 3.5  max singular value)
    Estimated rank (grad): 203
    GRAD: rank 203 computed from 203 data channels with 0 projectors

Compute the evoked response

Let’s just use the MEG channels for simplicity.

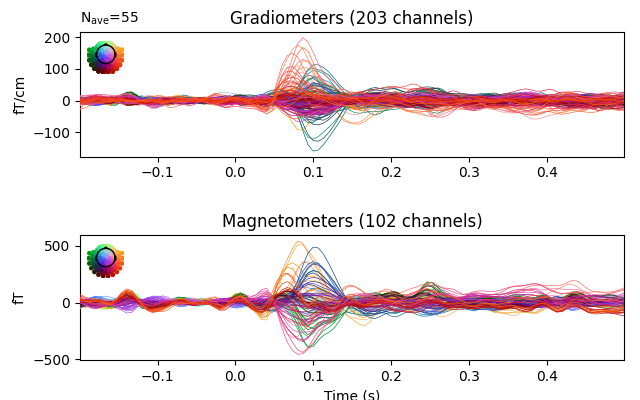
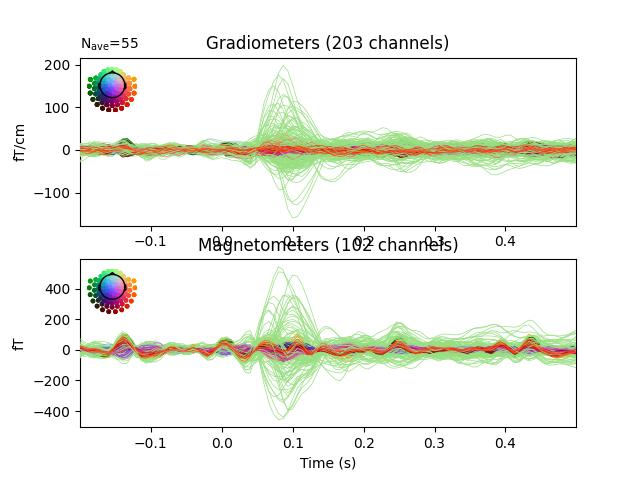
evoked = epochs.average().pick("meg")
evoked.plot(time_unit="s")
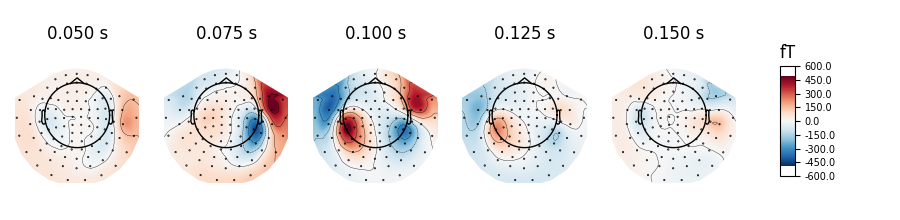
evoked.plot_topomap(times=np.linspace(0.05, 0.15, 5), ch_type="mag")

• 
• 

NOTE: pick_channels() is a legacy function. New code should use inst.pick(...).
Removing projector <Projection | Average EEG reference, active : True, n_channels : 60>

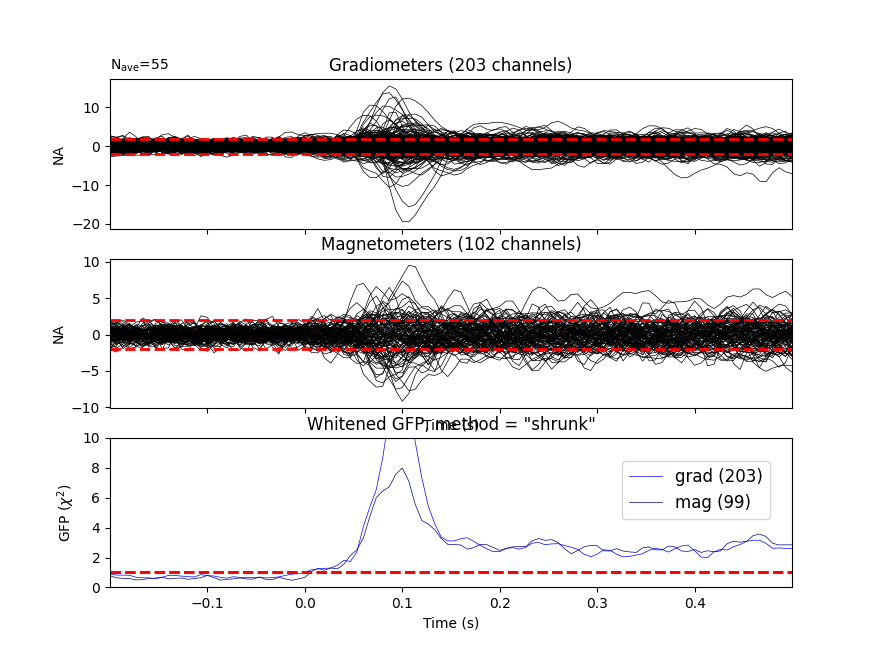
It’s also a good idea to look at whitened data:

evoked.plot_white(noise_cov, time_unit="s")
del epochs, raw  # to save memory

NOTE: pick_types() is a legacy function. New code should use inst.pick(...).
Computing rank from covariance with rank=None
    Using tolerance 1.6e-13 (2.2e-16 eps * 203 dim * 3.5  max singular value)
    Estimated rank (grad): 203
    GRAD: rank 203 computed from 203 data channels with 0 projectors
Computing rank from covariance with rank=None
    Using tolerance 2.2e-14 (2.2e-16 eps * 102 dim * 0.98  max singular value)
    Estimated rank (mag): 99
    MAG: rank 99 computed from 102 data channels with 3 projectors
    Created an SSP operator (subspace dimension = 3)
Computing rank from covariance with rank={'grad': 203, 'mag': 99, 'meg': 302}
    Setting small MEG eigenvalues to zero (without PCA)
    Created the whitener using a noise covariance matrix with rank 302 (3 small eigenvalues omitted)

Inverse modeling: MNE/dSPM on evoked and raw data

Here we first read the forward solution. You will likely need to compute one for your own data – see Head model and forward computation for information on how to do it.

fname_fwd = data_path / "MEG" / "sample" / "sample_audvis-meg-oct-6-fwd.fif"
fwd = mne.read_forward_solution(fname_fwd)

Reading forward solution from /home/circleci/mne_data/MNE-sample-data/MEG/sample/sample_audvis-meg-oct-6-fwd.fif...
    Reading a source space...
    Computing patch statistics...
    Patch information added...
    Distance information added...
    [done]
    Reading a source space...
    Computing patch statistics...
    Patch information added...
    Distance information added...
    [done]
    2 source spaces read
    Desired named matrix (kind = 3523) not available
    Read MEG forward solution (7498 sources, 306 channels, free orientations)
    Source spaces transformed to the forward solution coordinate frame

Next, we make an MEG inverse operator.

inverse_operator = make_inverse_operator(
    evoked.info, fwd, noise_cov, loose=0.2, depth=0.8
)
del fwd

# You can write it to disk with::
#
#     >>> from mne.minimum_norm import write_inverse_operator
#     >>> write_inverse_operator('sample_audvis-meg-oct-6-inv.fif',
#                                inverse_operator)

Converting forward solution to surface orientation
    Average patch normals will be employed in the rotation to the local surface coordinates....
    Converting to surface-based source orientations...
    [done]
info["bads"] and noise_cov["bads"] do not match, excluding bad channels from both
Computing inverse operator with 305 channels.
    305 out of 306 channels remain after picking
Selected 305 channels
Creating the depth weighting matrix...
    203 planar channels
    limit = 7265/7498 = 10.037795
    scale = 2.52065e-08 exp = 0.8
Applying loose dipole orientations to surface source spaces: 0.2
Whitening the forward solution.
    Created an SSP operator (subspace dimension = 3)
Computing rank from covariance with rank=None
    Using tolerance 2.9e-13 (2.2e-16 eps * 305 dim * 4.3  max singular value)
    Estimated rank (mag + grad): 302
    MEG: rank 302 computed from 305 data channels with 3 projectors
    Setting small MEG eigenvalues to zero (without PCA)
Creating the source covariance matrix
Adjusting source covariance matrix.
Computing SVD of whitened and weighted lead field matrix.
    largest singular value = 4.67933
    scaling factor to adjust the trace = 9.16538e+18 (nchan = 305 nzero = 3)

Compute inverse solution

We can use this to compute the inverse solution and obtain source time courses:

method = "dSPM"
snr = 3.0
lambda2 = 1.0 / snr**2
stc, residual = apply_inverse(
    evoked,
    inverse_operator,
    lambda2,
    method=method,
    pick_ori=None,
    return_residual=True,
    verbose=True,
)

Preparing the inverse operator for use...
    Scaled noise and source covariance from nave = 1 to nave = 55
    Created the regularized inverter
    Created an SSP operator (subspace dimension = 3)
    Created the whitener using a noise covariance matrix with rank 302 (3 small eigenvalues omitted)
    Computing noise-normalization factors (dSPM)...
[done]
Applying inverse operator to "aud_l"...
    Picked 305 channels from the data
    Computing inverse...
    Eigenleads need to be weighted ...
    Computing residual...
    Explained  65.2% variance
    Combining the current components...
    dSPM...
[done]

Visualization

We can look at different dipole activations:

fig, ax = plt.subplots()
ax.plot(1e3 * stc.times, stc.data[::100, :].T)
ax.set(xlabel="time (ms)", ylabel="%s value" % method)

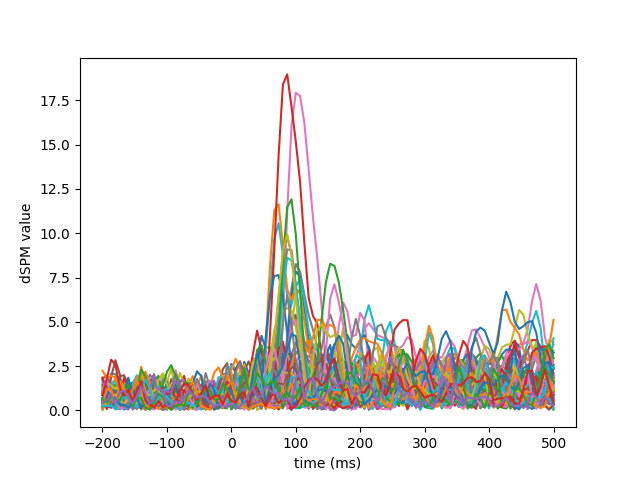
Examine the original data and the residual after fitting:

fig, axes = plt.subplots(2, 1)
evoked.plot(axes=axes)
for ax in axes:
    for text in list(ax.texts):
        text.remove()
    for line in ax.lines:
        line.set_color("#98df81")
residual.plot(axes=axes)

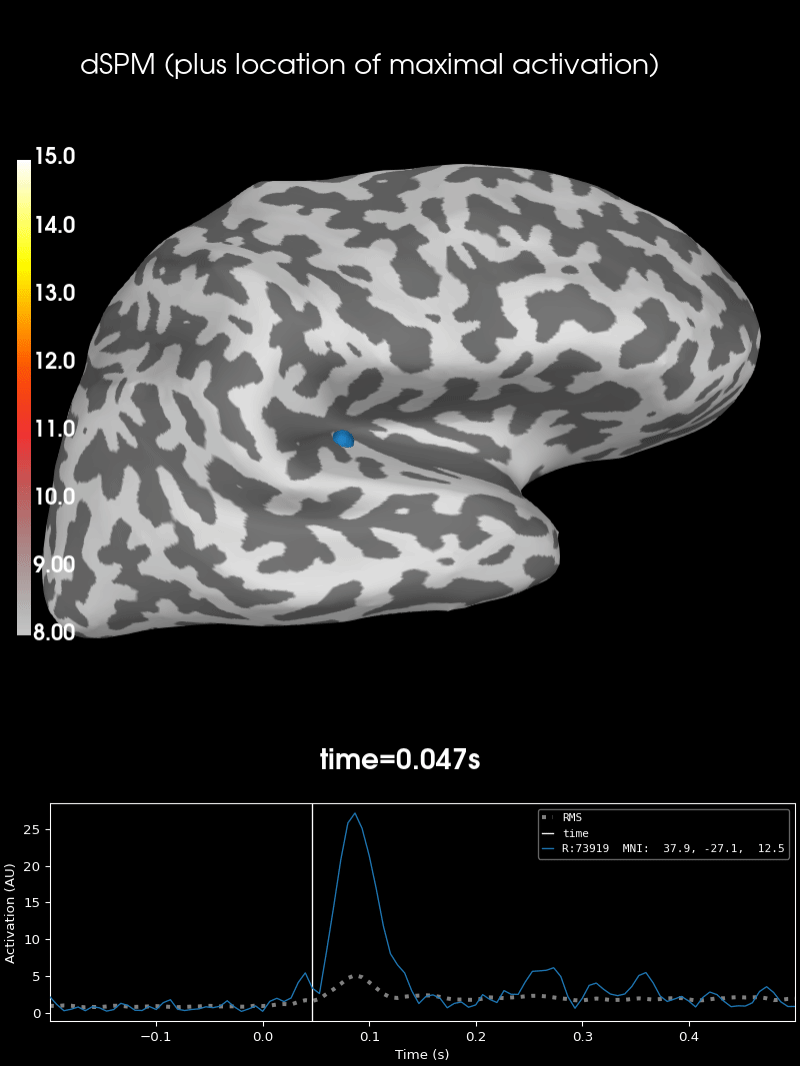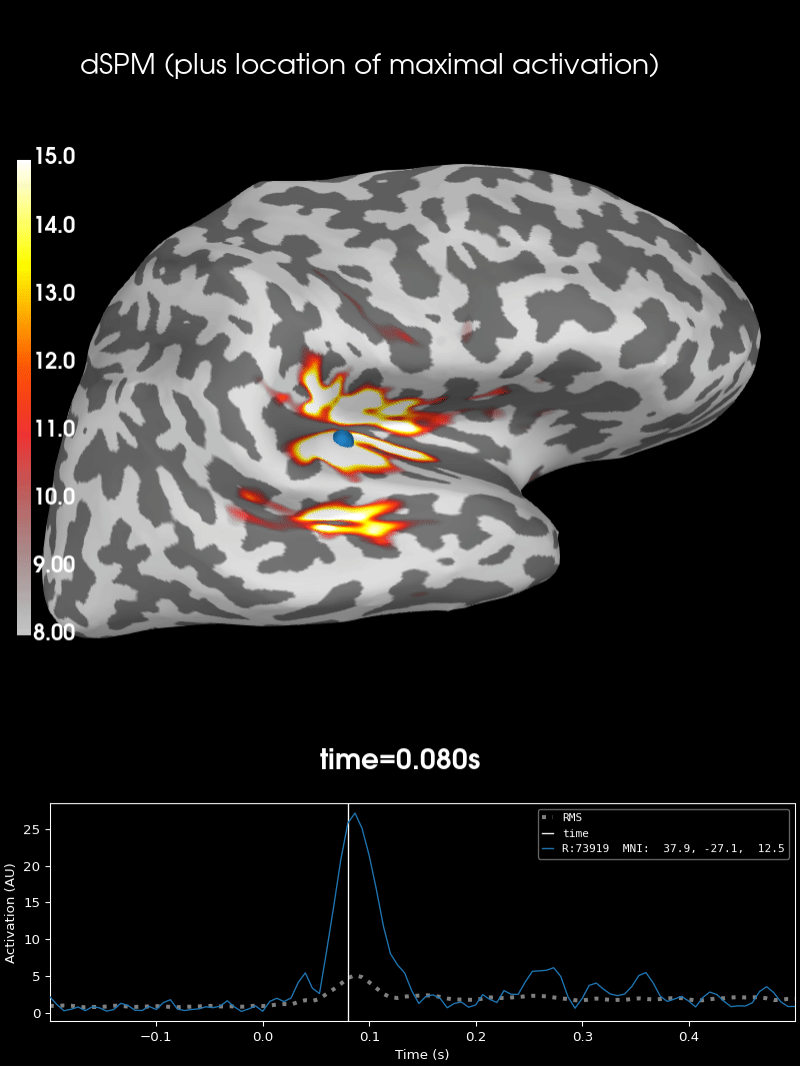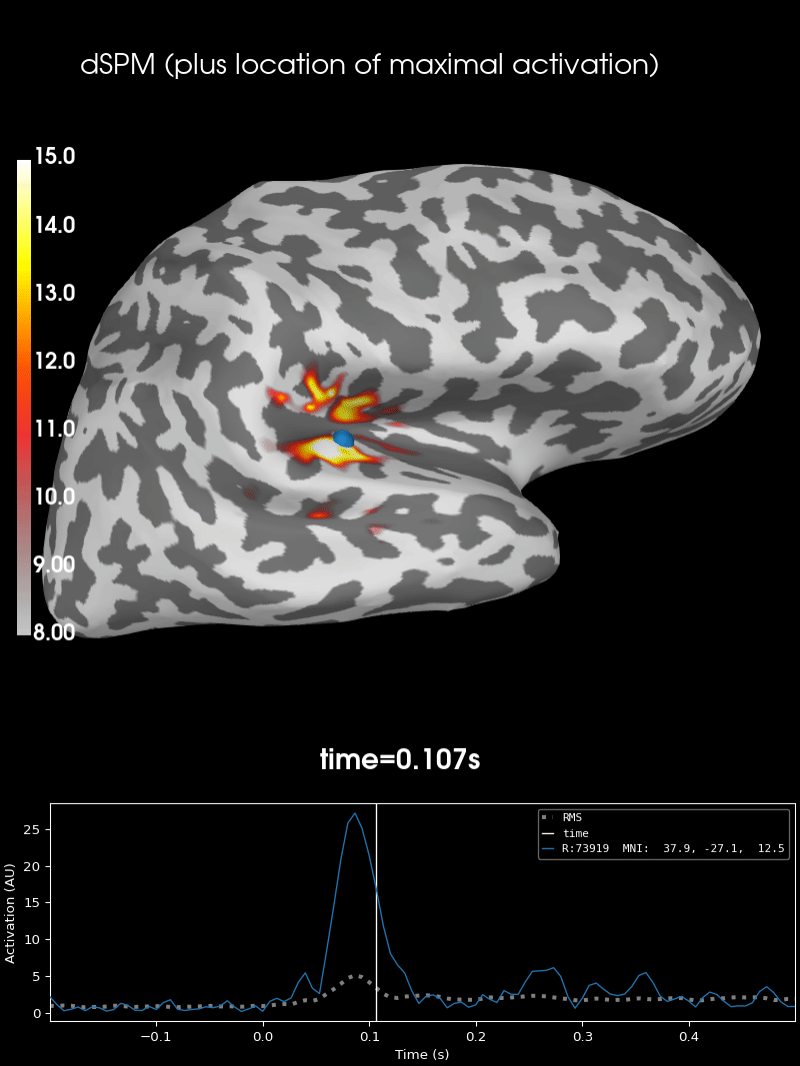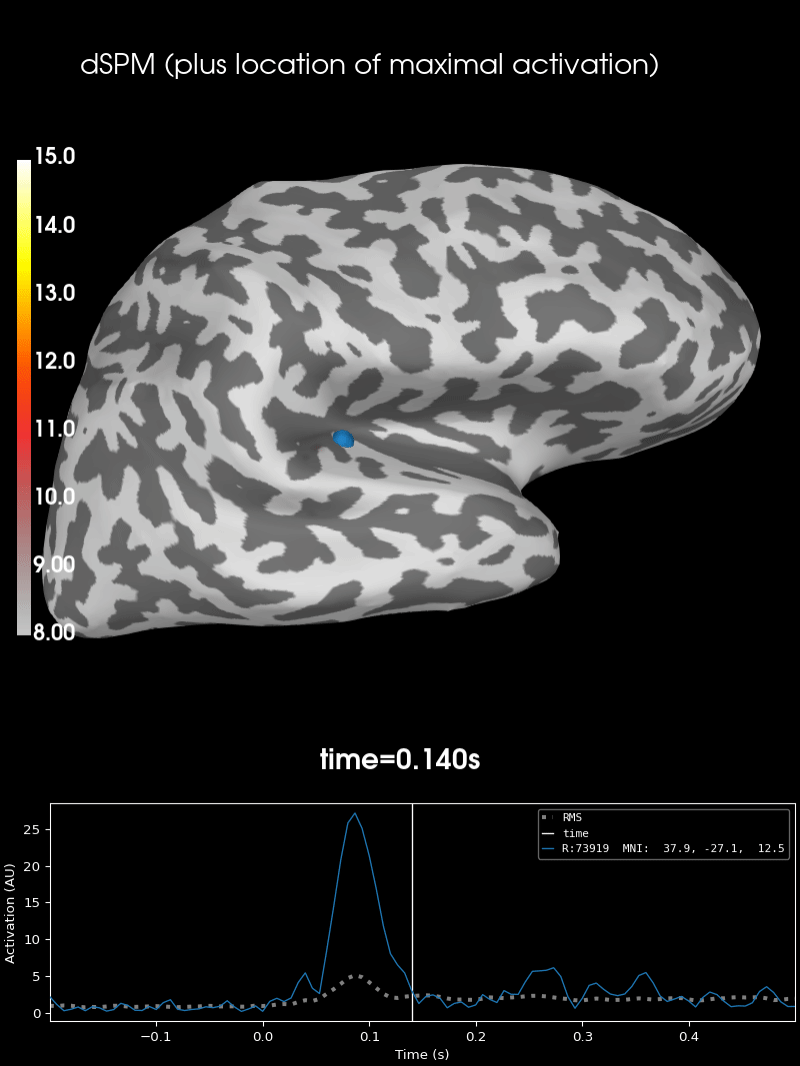
Here we use peak getter to move visualization to the time point of the peak and draw a marker at the maximum peak vertex.

vertno_max, time_max = stc.get_peak(hemi="rh")

subjects_dir = data_path / "subjects"
surfer_kwargs = dict(
    hemi="rh",
    subjects_dir=subjects_dir,
    clim=dict(kind="value", lims=[8, 12, 15]),
    views="lateral",
    initial_time=time_max,
    time_unit="s",
    size=(800, 800),
    smoothing_steps=10,
)
brain = stc.plot(**surfer_kwargs)
brain.add_foci(
    vertno_max,
    coords_as_verts=True,
    hemi="rh",
    color="blue",
    scale_factor=0.6,
    alpha=0.5,
)
brain.add_text(
    0.1, 0.9, "dSPM (plus location of maximal activation)", "title", font_size=14
)

# The documentation website's movie is generated with:
# brain.save_movie(..., tmin=0.05, tmax=0.15, interpolation='linear',
#                  time_dilation=20, framerate=10, time_viewer=True)

Once Loop Reflect

There are many other ways to visualize and work with source data, see for example:

• Visualize source time courses (stcs)

• Morph surface source estimate

• Morph volumetric source estimate

• Plotting the full vector-valued MNE solution

• The role of dipole orientations in distributed source localization

• Computing various MNE solutions

• examples using apply_inverse.

Estimated memory usage: 175 MB