Note
Click here to download the full example code
DICS for power mapping¶
In this tutorial, we’ll simulate two signals originating from two locations on the cortex. These signals will be sinusoids, so we’ll be looking at oscillatory activity (as opposed to evoked activity).
We’ll use dynamic imaging of coherent sources (DICS) 1 to map out spectral power along the cortex. Let’s see if we can find our two simulated sources.
# Author: Marijn van Vliet <w.m.vanvliet@gmail.com>
#
# License: BSD (3-clause)
Setup¶
We first import the required packages to run this tutorial and define a list of filenames for various things we’ll be using.
import os.path as op
import numpy as np
from scipy.signal import welch, coherence, unit_impulse
from matplotlib import pyplot as plt
import mne
from mne.simulation import simulate_raw, add_noise
from mne.datasets import sample
from mne.minimum_norm import make_inverse_operator, apply_inverse
from mne.time_frequency import csd_morlet
from mne.beamformer import make_dics, apply_dics_csd
# We use the MEG and MRI setup from the MNE-sample dataset
data_path = sample.data_path(download=False)
subjects_dir = op.join(data_path, 'subjects')
# Filenames for various files we'll be using
meg_path = op.join(data_path, 'MEG', 'sample')
raw_fname = op.join(meg_path, 'sample_audvis_raw.fif')
fwd_fname = op.join(meg_path, 'sample_audvis-meg-eeg-oct-6-fwd.fif')
cov_fname = op.join(meg_path, 'sample_audvis-cov.fif')
fwd = mne.read_forward_solution(fwd_fname)
# Seed for the random number generator
rand = np.random.RandomState(42)
Out:
Reading forward solution from /home/circleci/mne_data/MNE-sample-data/MEG/sample/sample_audvis-meg-eeg-oct-6-fwd.fif...
Reading a source space...
Computing patch statistics...
Patch information added...
Distance information added...
[done]
Reading a source space...
Computing patch statistics...
Patch information added...
Distance information added...
[done]
2 source spaces read
Desired named matrix (kind = 3523) not available
Read MEG forward solution (7498 sources, 306 channels, free orientations)
Desired named matrix (kind = 3523) not available
Read EEG forward solution (7498 sources, 60 channels, free orientations)
MEG and EEG forward solutions combined
Source spaces transformed to the forward solution coordinate frame
Data simulation¶
The following function generates a timeseries that contains an oscillator, whose frequency fluctuates a little over time, but stays close to 10 Hz. We’ll use this function to generate our two signals.
sfreq = 50. # Sampling frequency of the generated signal
n_samp = int(round(10. * sfreq))
times = np.arange(n_samp) / sfreq # 10 seconds of signal
n_times = len(times)
def coh_signal_gen():
"""Generate an oscillating signal.
Returns
-------
signal : ndarray
The generated signal.
"""
t_rand = 0.001 # Variation in the instantaneous frequency of the signal
std = 0.1 # Std-dev of the random fluctuations added to the signal
base_freq = 10. # Base frequency of the oscillators in Hertz
n_times = len(times)
# Generate an oscillator with varying frequency and phase lag.
signal = np.sin(2.0 * np.pi *
(base_freq * np.arange(n_times) / sfreq +
np.cumsum(t_rand * rand.randn(n_times))))
# Add some random fluctuations to the signal.
signal += std * rand.randn(n_times)
# Scale the signal to be in the right order of magnitude (~100 nAm)
# for MEG data.
signal *= 100e-9
return signal
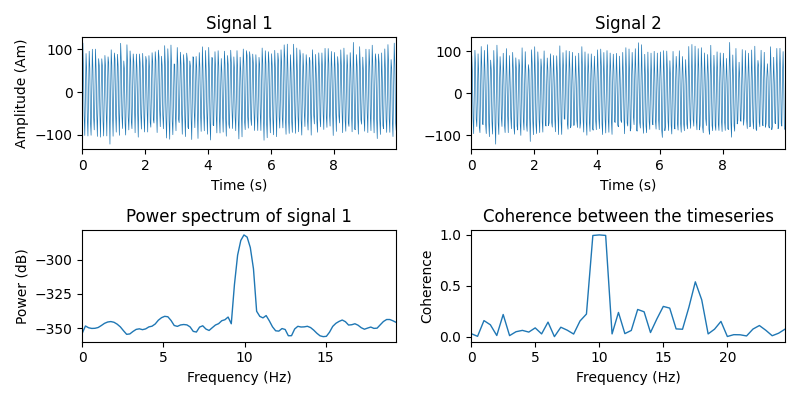
Let’s simulate two timeseries and plot some basic information about them.
signal1 = coh_signal_gen()
signal2 = coh_signal_gen()
fig, axes = plt.subplots(2, 2, figsize=(8, 4))
# Plot the timeseries
ax = axes[0][0]
ax.plot(times, 1e9 * signal1, lw=0.5)
ax.set(xlabel='Time (s)', xlim=times[[0, -1]], ylabel='Amplitude (Am)',
title='Signal 1')
ax = axes[0][1]
ax.plot(times, 1e9 * signal2, lw=0.5)
ax.set(xlabel='Time (s)', xlim=times[[0, -1]], title='Signal 2')
# Power spectrum of the first timeseries
f, p = welch(signal1, fs=sfreq, nperseg=128, nfft=256)
ax = axes[1][0]
# Only plot the first 100 frequencies
ax.plot(f[:100], 20 * np.log10(p[:100]), lw=1.)
ax.set(xlabel='Frequency (Hz)', xlim=f[[0, 99]],
ylabel='Power (dB)', title='Power spectrum of signal 1')
# Compute the coherence between the two timeseries
f, coh = coherence(signal1, signal2, fs=sfreq, nperseg=100, noverlap=64)
ax = axes[1][1]
ax.plot(f[:50], coh[:50], lw=1.)
ax.set(xlabel='Frequency (Hz)', xlim=f[[0, 49]], ylabel='Coherence',
title='Coherence between the timeseries')
fig.tight_layout()
Now we put the signals at two locations on the cortex. We construct a
mne.SourceEstimate object to store them in.
The timeseries will have a part where the signal is active and a part where it is not. The techniques we’ll be using in this tutorial depend on being able to contrast data that contains the signal of interest versus data that does not (i.e. it contains only noise).
# The locations on the cortex where the signal will originate from. These
# locations are indicated as vertex numbers.
vertices = [[146374], [33830]]
# Construct SourceEstimates that describe the signals at the cortical level.
data = np.vstack((signal1, signal2))
stc_signal = mne.SourceEstimate(
data, vertices, tmin=0, tstep=1. / sfreq, subject='sample')
stc_noise = stc_signal * 0.
Before we simulate the sensor-level data, let’s define a signal-to-noise ratio. You are encouraged to play with this parameter and see the effect of noise on our results.
snr = 1. # Signal-to-noise ratio. Decrease to add more noise.
Now we run the signal through the forward model to obtain simulated sensor data. To save computation time, we’ll only simulate gradiometer data. You can try simulating other types of sensors as well.
Some noise is added based on the baseline noise covariance matrix from the sample dataset, scaled to implement the desired SNR.
# Read the info from the sample dataset. This defines the location of the
# sensors and such.
info = mne.io.read_info(raw_fname)
info.update(sfreq=sfreq, bads=[])
# Only use gradiometers
picks = mne.pick_types(info, meg='grad', stim=True, exclude=())
mne.pick_info(info, picks, copy=False)
# Define a covariance matrix for the simulated noise. In this tutorial, we use
# a simple diagonal matrix.
cov = mne.cov.make_ad_hoc_cov(info)
cov['data'] *= (20. / snr) ** 2 # Scale the noise to achieve the desired SNR
# Simulate the raw data, with a lowpass filter on the noise
stcs = [(stc_signal, unit_impulse(n_samp, dtype=int) * 1),
(stc_noise, unit_impulse(n_samp, dtype=int) * 2)] # stacked in time
duration = (len(stc_signal.times) * 2) / sfreq
raw = simulate_raw(info, stcs, forward=fwd)
add_noise(raw, cov, iir_filter=[4, -4, 0.8], random_state=rand)
Out:
Read a total of 3 projection items:
PCA-v1 (1 x 102) idle
PCA-v2 (1 x 102) idle
PCA-v3 (1 x 102) idle
Setting up raw simulation: 1 position, "cos2" interpolation
Event information stored on channel: STI 014
Interval 0.000-10.000 sec
Setting up forward solutions
Computing gain matrix for transform #1/1
Interval 0.000-10.000 sec
2 STC iterations provided
Done
Adding noise to 204/213 channels (204 channels in cov)
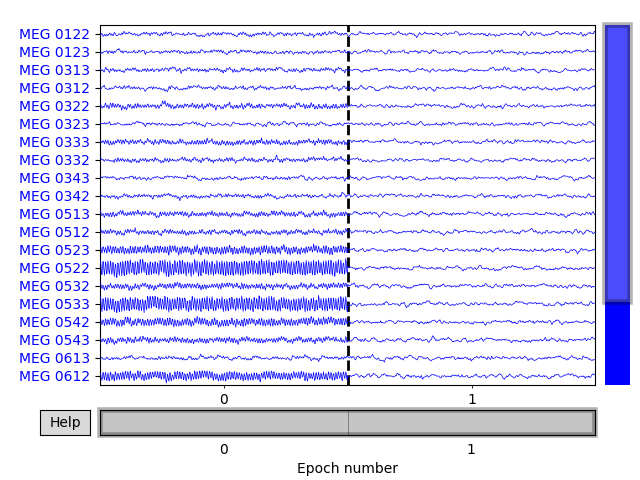
We create an mne.Epochs object containing two trials: one with
both noise and signal and one with just noise
events = mne.find_events(raw, initial_event=True)
tmax = (len(stc_signal.times) - 1) / sfreq
epochs = mne.Epochs(raw, events, event_id=dict(signal=1, noise=2),
tmin=0, tmax=tmax, baseline=None, preload=True)
assert len(epochs) == 2 # ensure that we got the two expected events
# Plot some of the channels of the simulated data that are situated above one
# of our simulated sources.
picks = mne.pick_channels(epochs.ch_names,
mne.read_vectorview_selection('Left-frontal'))
epochs.plot(picks=picks)
Out:
2 events found
Event IDs: [1 2]
Not setting metadata
Not setting metadata
2 matching events found
No baseline correction applied
3 projection items activated
Loading data for 2 events and 500 original time points ...
0 bad epochs dropped
Power mapping¶
With our simulated dataset ready, we can now pretend to be researchers that have just recorded this from a real subject and are going to study what parts of the brain communicate with each other.
First, we’ll create a source estimate of the MEG data. We’ll use both a straightforward MNE-dSPM inverse solution for this, and the DICS beamformer which is specifically designed to work with oscillatory data.
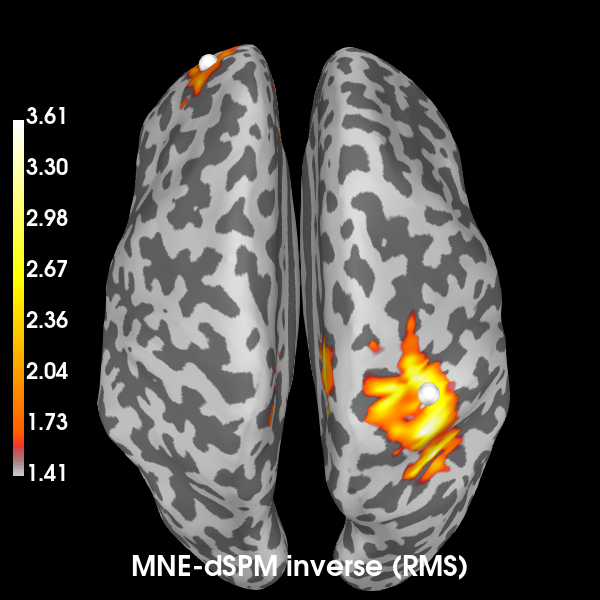
Computing the inverse using MNE-dSPM:
# Compute the inverse operator
fwd = mne.read_forward_solution(fwd_fname)
inv = make_inverse_operator(epochs.info, fwd, cov)
# Apply the inverse model to the trial that also contains the signal.
s = apply_inverse(epochs['signal'].average(), inv)
# Take the root-mean square along the time dimension and plot the result.
s_rms = np.sqrt((s ** 2).mean())
title = 'MNE-dSPM inverse (RMS)'
brain = s_rms.plot('sample', subjects_dir=subjects_dir, hemi='both', figure=1,
size=600, time_label=title, title=title)
# Indicate the true locations of the source activity on the plot.
brain.add_foci(vertices[0][0], coords_as_verts=True, hemi='lh')
brain.add_foci(vertices[1][0], coords_as_verts=True, hemi='rh')
# Rotate the view and add a title.
brain.show_view(view={'azimuth': 0, 'elevation': 0, 'distance': 550,
'focalpoint': [0, 0, 0]})
Out:
Reading forward solution from /home/circleci/mne_data/MNE-sample-data/MEG/sample/sample_audvis-meg-eeg-oct-6-fwd.fif...
Reading a source space...
Computing patch statistics...
Patch information added...
Distance information added...
[done]
Reading a source space...
Computing patch statistics...
Patch information added...
Distance information added...
[done]
2 source spaces read
Desired named matrix (kind = 3523) not available
Read MEG forward solution (7498 sources, 306 channels, free orientations)
Desired named matrix (kind = 3523) not available
Read EEG forward solution (7498 sources, 60 channels, free orientations)
MEG and EEG forward solutions combined
Source spaces transformed to the forward solution coordinate frame
Converting forward solution to surface orientation
Average patch normals will be employed in the rotation to the local surface coordinates....
Converting to surface-based source orientations...
[done]
Computing inverse operator with 204 channels.
204 out of 366 channels remain after picking
Selected 204 channels
Creating the depth weighting matrix...
204 planar channels
limit = 7261/7498 = 10.004929
scale = 2.59947e-08 exp = 0.8
Applying loose dipole orientations to surface source spaces: 0.2
Whitening the forward solution.
Computing rank from covariance with rank=None
Using tolerance 4.5e-14 (2.2e-16 eps * 204 dim * 1 max singular value)
Estimated rank (grad): 204
GRAD: rank 204 computed from 204 data channels with 0 projectors
Setting small GRAD eigenvalues to zero (without PCA)
Creating the source covariance matrix
Adjusting source covariance matrix.
Computing SVD of whitened and weighted lead field matrix.
largest singular value = 5.60587
scaling factor to adjust the trace = 2.91651e+18 (nchan = 204 nzero = 0)
Removing projector <Projection | PCA-v1, active : True, n_channels : 102>
Removing projector <Projection | PCA-v2, active : True, n_channels : 102>
Removing projector <Projection | PCA-v3, active : True, n_channels : 102>
Preparing the inverse operator for use...
Scaled noise and source covariance from nave = 1 to nave = 1
Created the regularized inverter
The projection vectors do not apply to these channels.
Created the whitener using a noise covariance matrix with rank 204 (0 small eigenvalues omitted)
Computing noise-normalization factors (dSPM)...
[done]
Applying inverse operator to "signal"...
Picked 204 channels from the data
Computing inverse...
Eigenleads need to be weighted ...
Computing residual...
Explained 75.0% variance
Combining the current components...
dSPM...
[done]
Using control points [1.41101364 1.65792783 3.61406449]
We will now compute the cortical power map at 10 Hz. using a DICS beamformer. A beamformer will construct for each vertex a spatial filter that aims to pass activity originating from the vertex, while dampening activity from other sources as much as possible.
The mne.beamformer.make_dics() function has many switches that offer
precise control
over the way the filter weights are computed. Currently, there is no clear
consensus regarding the best approach. This is why we will demonstrate two
approaches here:
# Estimate the cross-spectral density (CSD) matrix on the trial containing the
# signal.
csd_signal = csd_morlet(epochs['signal'], frequencies=[10])
# Compute the spatial filters for each vertex, using two approaches.
filters_approach1 = make_dics(
info, fwd, csd_signal, reg=0.05, pick_ori='max-power', depth=1.,
inversion='single', weight_norm=None, real_filter=True)
print(filters_approach1)
filters_approach2 = make_dics(
info, fwd, csd_signal, reg=0.05, pick_ori='max-power', depth=None,
inversion='matrix', weight_norm='unit-noise-gain', real_filter=True)
print(filters_approach2)
# You can save these to disk with:
# filters_approach1.save('filters_1-dics.h5')
# Compute the DICS power map by applying the spatial filters to the CSD matrix.
power_approach1, f = apply_dics_csd(csd_signal, filters_approach1)
power_approach2, f = apply_dics_csd(csd_signal, filters_approach2)
Out:
Removing projector <Projection | PCA-v1, active : True, n_channels : 102>
Removing projector <Projection | PCA-v2, active : True, n_channels : 102>
Removing projector <Projection | PCA-v3, active : True, n_channels : 102>
Computing cross-spectral density from epochs...
0%| | CSD epoch blocks : 0/1 [00:00<?, ?it/s]
100%|##########| CSD epoch blocks : 1/1 [00:00<00:00, 16.24it/s]
100%|##########| CSD epoch blocks : 1/1 [00:00<00:00, 16.14it/s]
[done]
Identifying common channels ...
Dropped the following channels:
['EEG 016', 'EEG 026', 'MEG 2641', 'MEG 2141', 'EEG 048', 'MEG 2021', 'MEG 1141', 'MEG 1441', 'MEG 1041', 'EEG 030', 'MEG 1821', 'EEG 028', 'MEG 0721', 'STI 002', 'EEG 017', 'EEG 002', 'MEG 2341', 'MEG 2441', 'MEG 1011', 'MEG 2131', 'MEG 0411', 'EEG 034', 'EEG 050', 'MEG 1121', 'MEG 1411', 'MEG 2241', 'MEG 1341', 'MEG 1421', 'MEG 2311', 'STI 006', 'EEG 055', 'MEG 0521', 'MEG 2611', 'MEG 1611', 'STI 014', 'MEG 2321', 'EEG 060', 'MEG 2011', 'EEG 003', 'MEG 2421', 'MEG 0241', 'MEG 0811', 'MEG 1731', 'MEG 0441', 'MEG 2541', 'MEG 1311', 'EEG 008', 'MEG 2411', 'EEG 044', 'MEG 0331', 'MEG 0231', 'MEG 2521', 'EEG 024', 'EEG 046', 'MEG 0741', 'MEG 0111', 'EEG 056', 'MEG 0341', 'MEG 0641', 'MEG 2511', 'STI 003', 'MEG 0921', 'EEG 033', 'EEG 049', 'EEG 011', 'MEG 1921', 'EEG 039', 'STI 015', 'MEG 1331', 'EEG 015', 'MEG 2431', 'MEG 2631', 'EEG 020', 'MEG 0131', 'EEG 053', 'MEG 1931', 'MEG 1521', 'EEG 005', 'MEG 1631', 'MEG 1431', 'EEG 031', 'MEG 1211', 'MEG 1831', 'MEG 1021', 'EEG 010', 'MEG 1241', 'EEG 006', 'EEG 037', 'MEG 0511', 'MEG 1811', 'EEG 023', 'MEG 0731', 'EEG 025', 'MEG 1941', 'MEG 0221', 'STI 016', 'EEG 013', 'EEG 032', 'MEG 0321', 'MEG 0941', 'MEG 2031', 'MEG 0121', 'STI 001', 'MEG 2231', 'EEG 038', 'EEG 040', 'EEG 027', 'EEG 054', 'EEG 036', 'EEG 019', 'MEG 1531', 'MEG 0531', 'MEG 1541', 'MEG 1131', 'MEG 0631', 'EEG 059', 'MEG 0211', 'EEG 007', 'MEG 1841', 'EEG 057', 'EEG 043', 'EEG 014', 'STI 005', 'EEG 045', 'MEG 2331', 'EEG 051', 'EEG 022', 'MEG 1741', 'MEG 1031', 'MEG 2041', 'EEG 035', 'MEG 0541', 'MEG 2531', 'EEG 012', 'MEG 0141', 'MEG 2221', 'EEG 058', 'EEG 042', 'MEG 1321', 'MEG 0911', 'EEG 018', 'MEG 0931', 'MEG 2121', 'MEG 1911', 'STI 004', 'MEG 0611', 'MEG 0421', 'MEG 0311', 'MEG 1721', 'MEG 1711', 'EEG 047', 'MEG 2621', 'EEG 004', 'EEG 009', 'MEG 1641', 'MEG 2211', 'MEG 1231', 'MEG 0711', 'MEG 0431', 'MEG 1111', 'EEG 021', 'EEG 029', 'MEG 2111', 'EEG 001', 'MEG 1621', 'MEG 0621', 'MEG 0821', 'MEG 1511', 'EEG 041', 'MEG 1221', 'EEG 052']
Computing inverse operator with 204 channels.
204 out of 204 channels remain after picking
Selected 204 channels
Creating the depth weighting matrix...
Whitening the forward solution.
Computing rank from covariance with rank=None
Using tolerance 4.5e+08 (2.2e-16 eps * 204 dim * 1e+22 max singular value)
Estimated rank (grad): 204
GRAD: rank 204 computed from 204 data channels with 0 projectors
Setting small GRAD eigenvalues to zero (without PCA)
Creating the source covariance matrix
Adjusting source covariance matrix.
Computing rank from covariance with rank=None
Using tolerance 1.5e-12 (2.2e-16 eps * 204 dim * 32 max singular value)
Estimated rank (grad): 139
GRAD: rank 139 computed from 204 data channels with 0 projectors
Computing DICS spatial filters...
Computing beamformer filters for 7498 sources
Filter computation complete
<Beamformer | DICS, subject "sample", 7498 vert, 204 ch, max-power ori, single inversion>
Identifying common channels ...
Dropped the following channels:
['EEG 016', 'EEG 026', 'MEG 2641', 'MEG 2141', 'EEG 048', 'MEG 2021', 'MEG 1141', 'MEG 1441', 'MEG 1041', 'EEG 030', 'MEG 1821', 'EEG 028', 'MEG 0721', 'STI 002', 'EEG 017', 'EEG 002', 'MEG 2341', 'MEG 2441', 'MEG 1011', 'MEG 2131', 'MEG 0411', 'EEG 034', 'EEG 050', 'MEG 1121', 'MEG 1411', 'MEG 2241', 'MEG 1341', 'MEG 1421', 'MEG 2311', 'STI 006', 'EEG 055', 'MEG 0521', 'MEG 2611', 'MEG 1611', 'STI 014', 'MEG 2321', 'EEG 060', 'MEG 2011', 'EEG 003', 'MEG 2421', 'MEG 0241', 'MEG 0811', 'MEG 1731', 'MEG 0441', 'MEG 2541', 'MEG 1311', 'EEG 008', 'MEG 2411', 'EEG 044', 'MEG 0331', 'MEG 0231', 'MEG 2521', 'EEG 024', 'EEG 046', 'MEG 0741', 'MEG 0111', 'EEG 056', 'MEG 0341', 'MEG 0641', 'MEG 2511', 'STI 003', 'MEG 0921', 'EEG 033', 'EEG 049', 'EEG 011', 'MEG 1921', 'EEG 039', 'STI 015', 'MEG 1331', 'EEG 015', 'MEG 2431', 'MEG 2631', 'EEG 020', 'MEG 0131', 'EEG 053', 'MEG 1931', 'MEG 1521', 'EEG 005', 'MEG 1631', 'MEG 1431', 'EEG 031', 'MEG 1211', 'MEG 1831', 'MEG 1021', 'EEG 010', 'MEG 1241', 'EEG 006', 'EEG 037', 'MEG 0511', 'MEG 1811', 'EEG 023', 'MEG 0731', 'EEG 025', 'MEG 1941', 'MEG 0221', 'STI 016', 'EEG 013', 'EEG 032', 'MEG 0321', 'MEG 0941', 'MEG 2031', 'MEG 0121', 'STI 001', 'MEG 2231', 'EEG 038', 'EEG 040', 'EEG 027', 'EEG 054', 'EEG 036', 'EEG 019', 'MEG 1531', 'MEG 0531', 'MEG 1541', 'MEG 1131', 'MEG 0631', 'EEG 059', 'MEG 0211', 'EEG 007', 'MEG 1841', 'EEG 057', 'EEG 043', 'EEG 014', 'STI 005', 'EEG 045', 'MEG 2331', 'EEG 051', 'EEG 022', 'MEG 1741', 'MEG 1031', 'MEG 2041', 'EEG 035', 'MEG 0541', 'MEG 2531', 'EEG 012', 'MEG 0141', 'MEG 2221', 'EEG 058', 'EEG 042', 'MEG 1321', 'MEG 0911', 'EEG 018', 'MEG 0931', 'MEG 2121', 'MEG 1911', 'STI 004', 'MEG 0611', 'MEG 0421', 'MEG 0311', 'MEG 1721', 'MEG 1711', 'EEG 047', 'MEG 2621', 'EEG 004', 'EEG 009', 'MEG 1641', 'MEG 2211', 'MEG 1231', 'MEG 0711', 'MEG 0431', 'MEG 1111', 'EEG 021', 'EEG 029', 'MEG 2111', 'EEG 001', 'MEG 1621', 'MEG 0621', 'MEG 0821', 'MEG 1511', 'EEG 041', 'MEG 1221', 'EEG 052']
Computing inverse operator with 204 channels.
204 out of 204 channels remain after picking
Selected 204 channels
Whitening the forward solution.
Computing rank from covariance with rank=None
Using tolerance 4.5e+08 (2.2e-16 eps * 204 dim * 1e+22 max singular value)
Estimated rank (grad): 204
GRAD: rank 204 computed from 204 data channels with 0 projectors
Setting small GRAD eigenvalues to zero (without PCA)
Creating the source covariance matrix
Adjusting source covariance matrix.
Computing rank from covariance with rank=None
Using tolerance 1.5e-12 (2.2e-16 eps * 204 dim * 32 max singular value)
Estimated rank (grad): 139
GRAD: rank 139 computed from 204 data channels with 0 projectors
Computing DICS spatial filters...
Computing beamformer filters for 7498 sources
Filter computation complete
<Beamformer | DICS, subject "sample", 7498 vert, 204 ch, max-power ori, unit-noise-gain norm, matrix inversion>
Computing DICS source power...
[done]
Computing DICS source power...
[done]
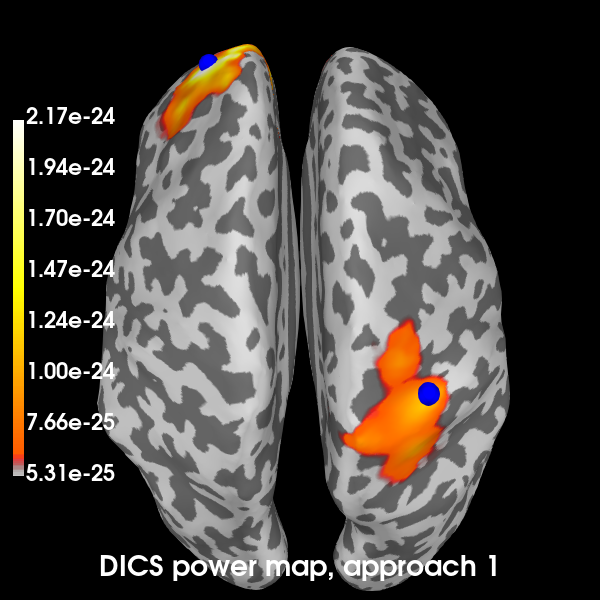
Plot the DICS power maps for both approaches, starting with the first:
def plot_approach(power, n):
"""Plot the results on a brain."""
title = 'DICS power map, approach %d' % n
brain = power_approach1.plot(
'sample', subjects_dir=subjects_dir, hemi='both',
size=600, time_label=title, title=title)
# Indicate the true locations of the source activity on the plot.
brain.add_foci(vertices[0][0], coords_as_verts=True, hemi='lh', color='b')
brain.add_foci(vertices[1][0], coords_as_verts=True, hemi='rh', color='b')
# Rotate the view and add a title.
brain.show_view(view={'azimuth': 0, 'elevation': 0, 'distance': 550,
'focalpoint': [0, 0, 0]})
return brain
brain1 = plot_approach(power_approach1, 1)
Out:
Using control points [5.31458766e-25 6.31530886e-25 2.17335209e-24]
Now the second:
brain2 = plot_approach(power_approach2, 2)
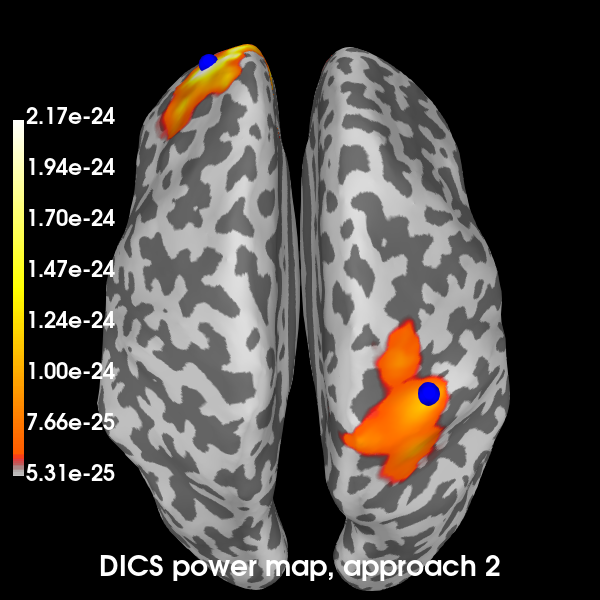
Out:
Using control points [5.31458766e-25 6.31530886e-25 2.17335209e-24]
Excellent! All methods found our two simulated sources. Of course, with a signal-to-noise ratio (SNR) of 1, is isn’t very hard to find them. You can try playing with the SNR and see how the MNE-dSPM and DICS approaches hold up in the presence of increasing noise. In the presence of more noise, you may need to increase the regularization parameter of the DICS beamformer.
References¶
- 1
Joachim Groß, Jan Kujala, Matti S. Hämäläinen, Lars Timmermann, Alfons Schnitzler, and Riitta Salmelin. Dynamic imaging of coherent sources: studying neural interactions in the human brain. Proceedings of the National Academy of Sciences, 98(2):694–699, 2001. doi:10.1073/pnas.98.2.694.
- 2
Marijn van Vliet, Mia Liljeström, Susanna Aro, Riitta Salmelin, and Jan Kujala. Analysis of functional connectivity and oscillatory power using DICS: from raw MEG data to group-level statistics in Python. bioRxiv, 2018. doi:10.1101/245530.
- 3
Kensuke Sekihara and Srikantan S. Nagarajan. Adaptive Spatial Filters for Electromagnetic Brain Imaging. Series in Biomedical Engineering. Springer, Berlin; Heidelberg, 2008. ISBN 978-3-540-79369-4 978-3-540-79370-0. doi:10.1007/978-3-540-79370-0.
Total running time of the script: ( 0 minutes 41.578 seconds)
Estimated memory usage: 312 MB