EEG processing and Event Related Potentials (ERPs)

This tutorial shows how to perform standard ERP analyses in MNE-Python. Most of the material here is covered in other tutorials too, but for convenience the functions and methods most useful for ERP analyses are collected here, with links to other tutorials where more detailed information is given.

As usual we’ll start by importing the modules we need and loading some example data. Instead of parsing the events from the raw data’s stim channel (like we do in this tutorial), we’ll load the events from an external events file. Finally, to speed up computations so our documentation server can handle them, we’ll crop the raw data from ~4.5 minutes down to 90 seconds.

import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import mne

sample_data_folder = mne.datasets.sample.data_path()
sample_data_raw_file = os.path.join(sample_data_folder, 'MEG', 'sample',
                                    'sample_audvis_filt-0-40_raw.fif')
raw = mne.io.read_raw_fif(sample_data_raw_file, preload=False)

sample_data_events_file = os.path.join(sample_data_folder, 'MEG', 'sample',
                                       'sample_audvis_filt-0-40_raw-eve.fif')
events = mne.read_events(sample_data_events_file)

raw.crop(tmax=90)  # in seconds; happens in-place
# discard events >90 seconds (not strictly necessary: avoids some warnings)
events = events[events[:, 0] <= raw.last_samp]

Out:

Opening raw data file /home/circleci/mne_data/MNE-sample-data/MEG/sample/sample_audvis_filt-0-40_raw.fif...
    Read a total of 4 projection items:
        PCA-v1 (1 x 102)  idle
        PCA-v2 (1 x 102)  idle
        PCA-v3 (1 x 102)  idle
        Average EEG reference (1 x 60)  idle
    Range : 6450 ... 48149 =     42.956 ...   320.665 secs
Ready.

The file that we loaded has already been partially processed: 3D sensor locations have been saved as part of the .fif file, the data have been low-pass filtered at 40 Hz, and a common average reference is set for the EEG channels, stored as a projector (see Creating the average reference as a projector in the Setting the EEG reference tutorial for more info about when you may want to do this). We’ll discuss how to do each of these below.

Since this is a combined EEG+MEG dataset, let’s start by restricting the data to just the EEG and EOG channels. This will cause the other projectors saved in the file (which apply only to magnetometer channels) to be removed. By looking at the measurement info we can see that we now have 59 EEG channels and 1 EOG channel.

raw.pick(['eeg', 'eog']).load_data()
raw.info

Out:

Removing projector <Projection | PCA-v1, active : False, n_channels : 102>
Removing projector <Projection | PCA-v2, active : False, n_channels : 102>
Removing projector <Projection | PCA-v3, active : False, n_channels : 102>
Reading 0 ... 13514  =      0.000 ...    90.001 secs...

Measurement date	December 03, 2002 19:01:10 GMT
Experimenter	Unknown
Participant	Unknown
Digitized points	146 points
Good channels	60 EEG, 1 EOG
Bad channels	EEG 053
EOG channels	EOG 061
ECG channels	Not available
Sampling frequency	150.15 Hz
Highpass	0.10 Hz
Lowpass	40.00 Hz
Projections	Average EEG reference: off

Channel names and types

In practice it’s quite common to have some channels labelled as EEG that are actually EOG channels. Raw objects have a set_channel_types method that you can use to change a channel that is labeled as eeg into an eog type. You can also rename channels using the rename_channels method. Detailed examples of both of these methods can be found in the tutorial The Raw data structure: continuous data. In this data the channel types are all correct already, so for now we’ll just rename the channels to remove a space and a leading zero in the channel names, and convert to lowercase:

channel_renaming_dict = {name: name.replace(' 0', '').lower()
                         for name in raw.ch_names}
_ = raw.rename_channels(channel_renaming_dict)  # happens in-place

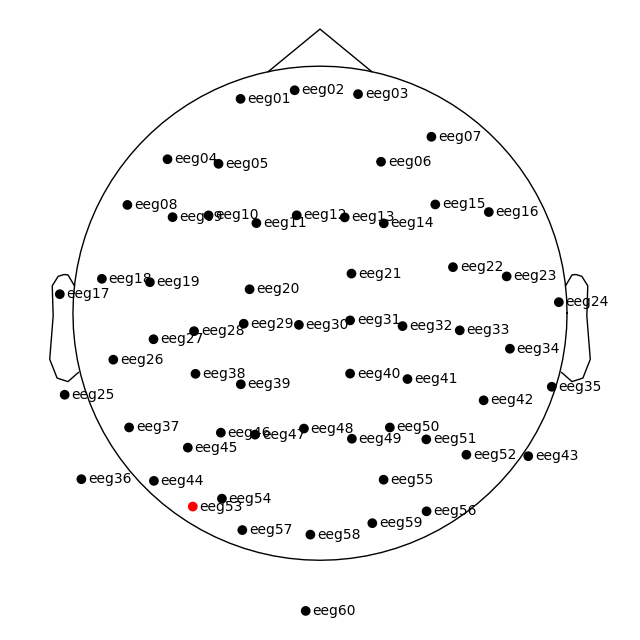
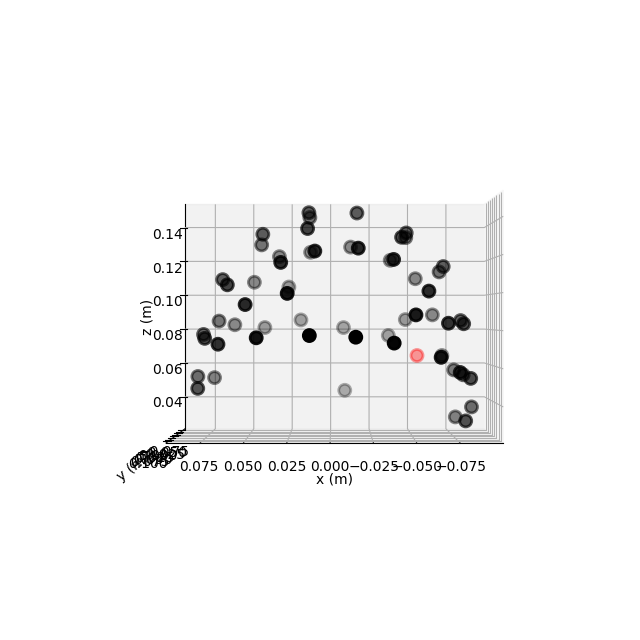
Channel locations

The tutorial Working with sensor locations describes MNE-Python’s handling of sensor positions in great detail. To briefly summarize: MNE-Python distinguishes montages (which contain sensor positions in 3D: x, y, z, in meters) from layouts (which define 2D arrangements of sensors for plotting approximate overhead diagrams of sensor positions). Additionally, montages may specify idealized sensor positions (based on, e.g., an idealized spherical headshape model) or they may contain realistic sensor positions obtained by digitizing the 3D locations of the sensors when placed on the actual subject’s head.

This dataset has realistic digitized 3D sensor locations saved as part of the .fif file, so we can view the sensor locations in 2D or 3D using the plot_sensors method:

raw.plot_sensors(show_names=True)
fig = raw.plot_sensors('3d')

• 
• 

If you’re working with a standard montage like the 10-20 system, you can add sensor locations to the data like this: raw.set_montage('standard_1020'). See Working with sensor locations for info on what other standard montages are built-in to MNE-Python.

If you have digitized realistic sensor locations, there are dedicated functions for loading those digitization files into MNE-Python; see Reading sensor digitization files for discussion and Supported formats for digitized 3D locations for a list of supported formats. Once loaded, the digitized sensor locations can be added to the data by passing the loaded montage object to raw.set_montage().

Setting the EEG reference

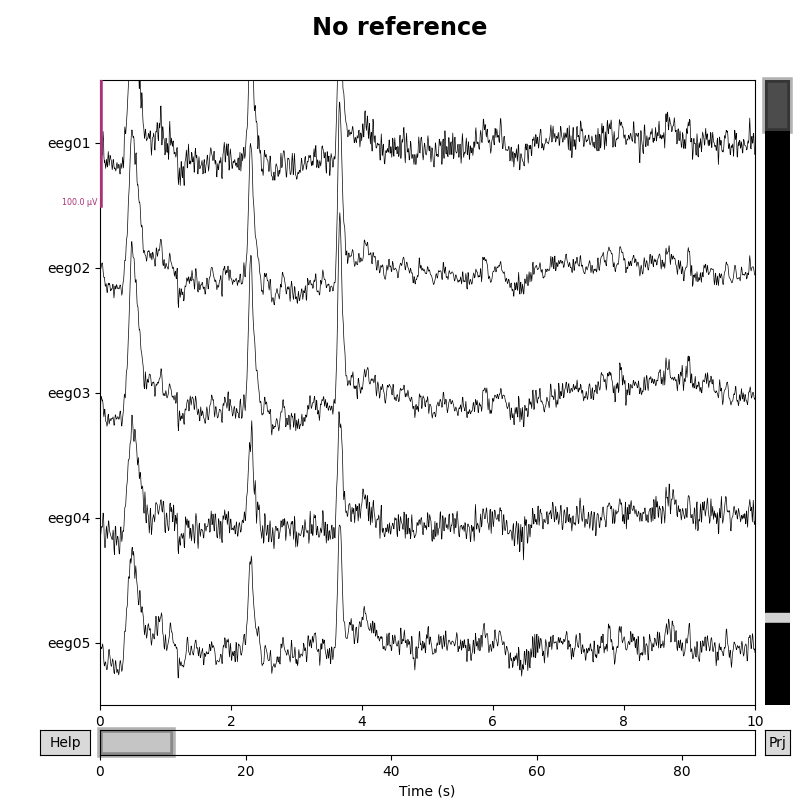
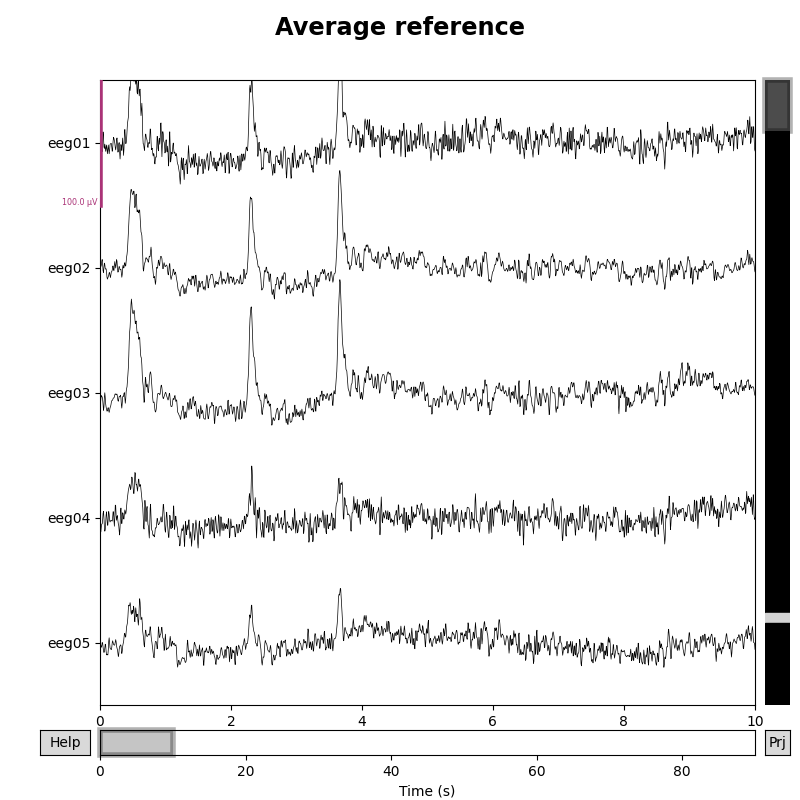
As mentioned above, this data already has an EEG common average reference added as a projector. We can view the effect of this on the raw data by plotting with and without the projector applied:

for proj in (False, True):
    fig = raw.plot(n_channels=5, proj=proj, scalings=dict(eeg=50e-6))
    fig.subplots_adjust(top=0.9)  # make room for title
    ref = 'Average' if proj else 'No'
    fig.suptitle(f'{ref} reference', size='xx-large', weight='bold')

• 
• 

The referencing scheme can be changed with the function mne.set_eeg_reference (which by default operates on a copy of the data) or the raw.set_eeg_reference() method (which always modifies the data in-place). The tutorial Setting the EEG reference shows several examples of this.

Filtering

MNE-Python has extensive support for different ways of filtering data. For a general discussion of filter characteristics and MNE-Python defaults, see Background information on filtering. For practical examples of how to apply filters to your data, see Filtering and resampling data. Here, we’ll apply a simple high-pass filter for illustration:

raw.filter(l_freq=0.1, h_freq=None)

Out:

Filtering raw data in 1 contiguous segment
Setting up high-pass filter at 0.1 Hz

FIR filter parameters
---------------------
Designing a one-pass, zero-phase, non-causal highpass filter:
- Windowed time-domain design (firwin) method
- Hamming window with 0.0194 passband ripple and 53 dB stopband attenuation
- Lower passband edge: 0.10
- Lower transition bandwidth: 0.10 Hz (-6 dB cutoff frequency: 0.05 Hz)
- Filter length: 4957 samples (33.013 sec)

Measurement date	December 03, 2002 19:01:10 GMT
Experimenter	Unknown
Participant	Unknown
Digitized points	146 points
Good channels	60 EEG, 1 EOG
Bad channels	eeg53
EOG channels	eog61
ECG channels	Not available
Sampling frequency	150.15 Hz
Highpass	0.10 Hz
Lowpass	40.00 Hz
Projections	Average EEG reference: off
Filenames	sample_audvis_filt-0-40_raw.fif
Duration	00:01:30 (HH:MM:SS)

Evoked responses: epoching and averaging

The general process for extracting evoked responses from continuous data is to use the Epochs constructor, and then average the resulting epochs to create an Evoked object. In MNE-Python, events are represented as a NumPy array of sample numbers and integer event codes. The event codes are stored in the last column of the events array:

np.unique(events[:, -1])

The Working with events tutorial discusses event arrays in more detail. Integer event codes are mapped to more descriptive text using a Python dictionary usually called event_id. This mapping is determined by your experiment code (i.e., it reflects which event codes you chose to use to represent different experimental events or conditions). For the Sample data has the following mapping:

event_dict = {'auditory/left': 1, 'auditory/right': 2, 'visual/left': 3,
              'visual/right': 4, 'face': 5, 'buttonpress': 32}

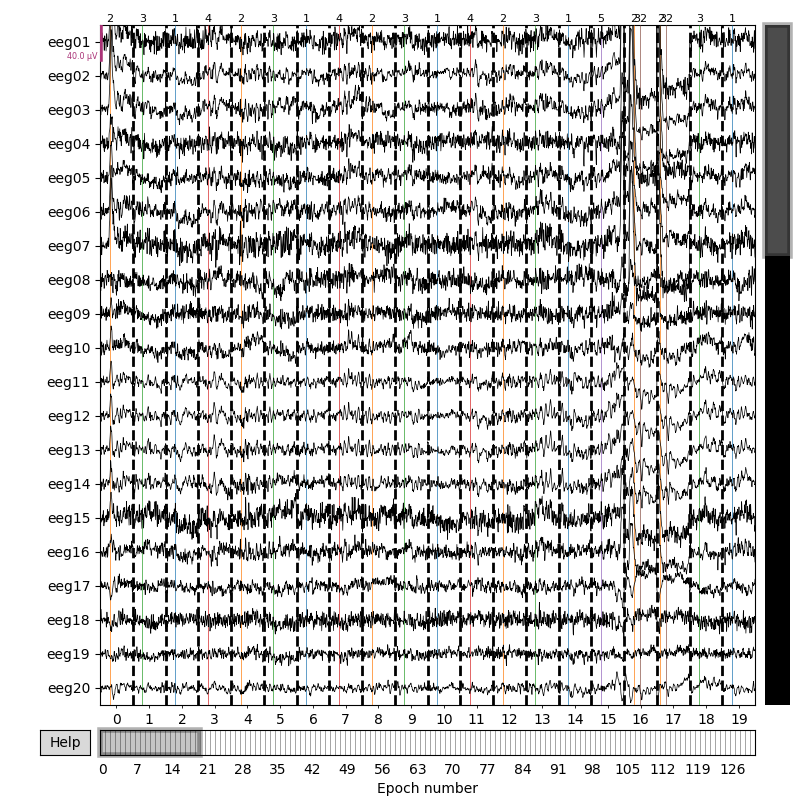
Now we can extract epochs from the continuous data. An interactive plot allows you to click on epochs to mark them as “bad” and drop them from the analysis (it is not interactive on the documentation website, but will be when you run epochs.plot() in a Python console).

epochs = mne.Epochs(raw, events, event_id=event_dict, tmin=-0.3, tmax=0.7,
                    preload=True)
fig = epochs.plot(events=events)

Out:

Not setting metadata
Not setting metadata
132 matching events found
Setting baseline interval to [-0.2996928197375818, 0.0] sec
Applying baseline correction (mode: mean)
Created an SSP operator (subspace dimension = 1)
1 projection items activated
Loading data for 132 events and 151 original time points ...
1 bad epochs dropped
You seem to have overlapping epochs. Some event lines may be duplicated in the plot.

It is also possible to automatically drop epochs, when first creating them or later on, by providing maximum peak-to-peak signal value thresholds (pass to the Epochs constructor as the reject parameter; see Rejecting Epochs based on channel amplitude for details). You can also do this after the epochs are already created, using the drop_bad method:

reject_criteria = dict(eeg=100e-6,  # 100 µV
                       eog=200e-6)  # 200 µV
_ = epochs.drop_bad(reject=reject_criteria)

Out:

    Rejecting  epoch based on EEG : ['eeg03']
    Rejecting  epoch based on EEG : ['eeg01', 'eeg02', 'eeg03', 'eeg04', 'eeg06', 'eeg07']
    Rejecting  epoch based on EEG : ['eeg01', 'eeg02', 'eeg03', 'eeg04', 'eeg06', 'eeg07']
    Rejecting  epoch based on EEG : ['eeg01', 'eeg02', 'eeg03', 'eeg04', 'eeg06', 'eeg07']
    Rejecting  epoch based on EEG : ['eeg01', 'eeg02', 'eeg03', 'eeg07']
    Rejecting  epoch based on EEG : ['eeg01', 'eeg02', 'eeg03', 'eeg07']
    Rejecting  epoch based on EEG : ['eeg01']
    Rejecting  epoch based on EEG : ['eeg03', 'eeg07']
    Rejecting  epoch based on EEG : ['eeg03', 'eeg07']
    Rejecting  epoch based on EEG : ['eeg07']
    Rejecting  epoch based on EEG : ['eeg03', 'eeg07']
    Rejecting  epoch based on EEG : ['eeg03', 'eeg07']
    Rejecting  epoch based on EEG : ['eeg07']
    Rejecting  epoch based on EEG : ['eeg07']
    Rejecting  epoch based on EEG : ['eeg03']
    Rejecting  epoch based on EEG : ['eeg25']
    Rejecting  epoch based on EEG : ['eeg25']
17 bad epochs dropped

Next we generate a barplot of which channels contributed most to epochs getting rejected. If one channel is responsible for lots of epoch rejections, it may be worthwhile to mark that channel as “bad” in the Raw object and then re-run epoching (fewer channels w/ more good epochs may be preferable to keeping all channels but losing many epochs). See Handling bad channels for more info.

epochs.plot_drop_log()

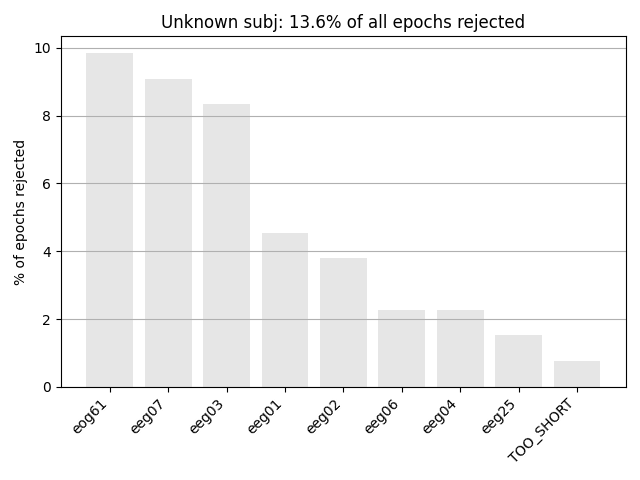
Another way in which epochs can be automatically dropped is if the event around which the epoch is formed is too close to the start or end of the Raw object (e.g., if the epoch’s tmax would be past the end of the file; this is the cause of the “TOO_SHORT” entry in the plot_drop_log plot above). Epochs may also be automatically dropped if the Raw object contains annotations that begin with either bad or edge (“edge” annotations are automatically inserted when concatenating two separate Raw objects together). See Rejecting bad data spans and breaks for more information about annotation-based epoch rejection.

Now that we’ve dropped the bad epochs, let’s look at our evoked responses for some conditions we care about. Here the average method will create an Evoked object, which we can then plot. Notice that we select which condition we want to average using the square-bracket indexing (like a dictionary); that returns a smaller epochs object containing just the epochs from that condition, to which we then apply the average method:

l_aud = epochs['auditory/left'].average()
l_vis = epochs['visual/left'].average()

These Evoked objects have their own interactive plotting method (though again, it won’t be interactive on the documentation website): click-dragging a span of time will generate a scalp field topography for that time span. Here we also demonstrate built-in color-coding the channel traces by location:

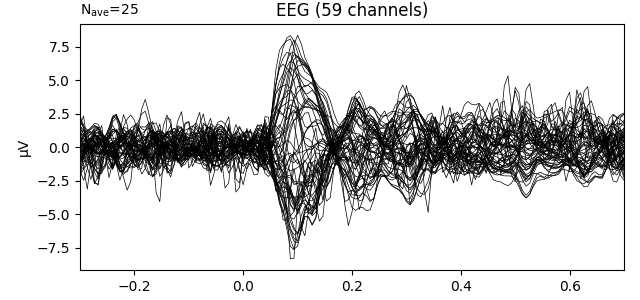
fig1 = l_aud.plot()
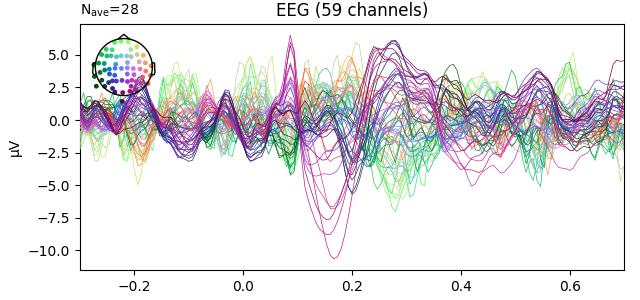
fig2 = l_vis.plot(spatial_colors=True)

• 
• 

Scalp topographies can also be obtained non-interactively with the plot_topomap method. Here we display topomaps of the average field in 50 ms time windows centered at -200 ms, 100 ms, and 400 ms.

l_aud.plot_topomap(times=[-0.2, 0.1, 0.4], average=0.05)

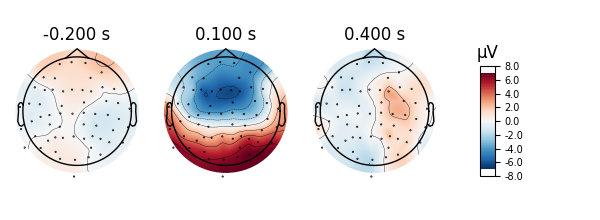
Considerable customization of these plots is possible, see the docstring of plot_topomap for details.

There is also a built-in method for combining “butterfly” plots of the signals with scalp topographies, called plot_joint. Like plot_topomap you can specify times for the scalp topographies or you can let the method choose times automatically, as is done here:

l_aud.plot_joint()

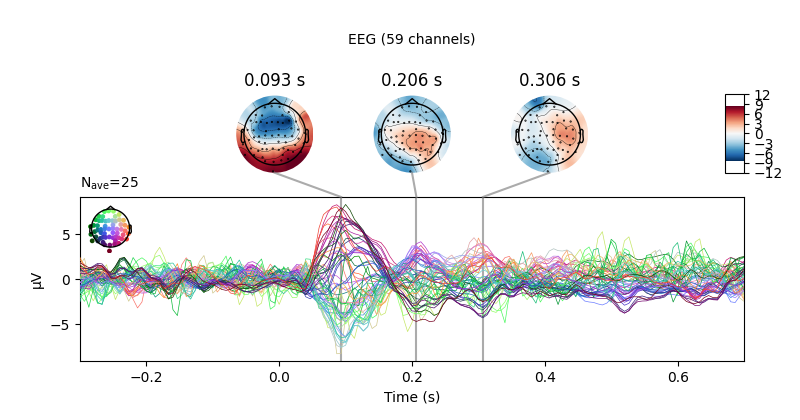
Out:

Projections have already been applied. Setting proj attribute to True.

Global field power (GFP)

Global field power 123 is, generally speaking, a measure of agreement of the signals picked up by all sensors across the entire scalp: if all sensors have the same value at a given time point, the GFP will be zero at that time point; if the signals differ, the GFP will be non-zero at that time point. GFP peaks may reflect “interesting” brain activity, warranting further investigation. Mathematically, the GFP is the population standard deviation across all sensors, calculated separately for every time point.

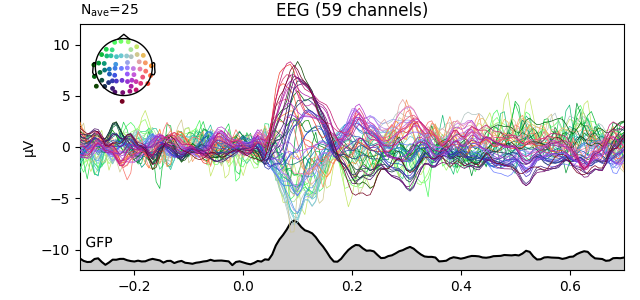
You can plot the GFP using evoked.plot(gfp=True). The GFP trace will be black if spatial_colors=True and green otherwise. The EEG reference does not affect the GFP:

for evk in (l_aud, l_vis):
    evk.plot(gfp=True, spatial_colors=True, ylim=dict(eeg=[-12, 12]))

• 
• 

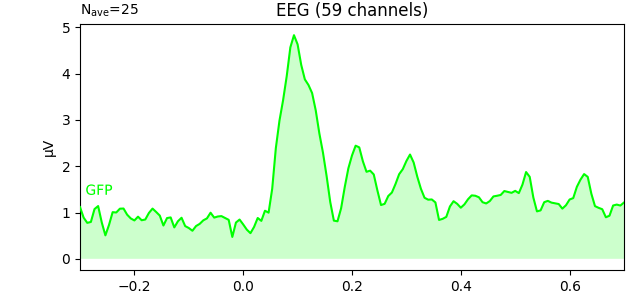
To plot the GFP by itself you can pass gfp='only' (this makes it easier to read off the GFP data values, because the scale is aligned):

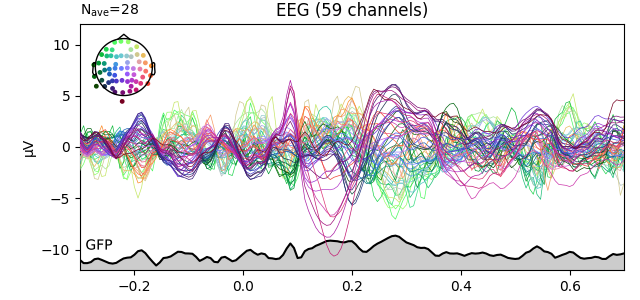
l_aud.plot(gfp='only')

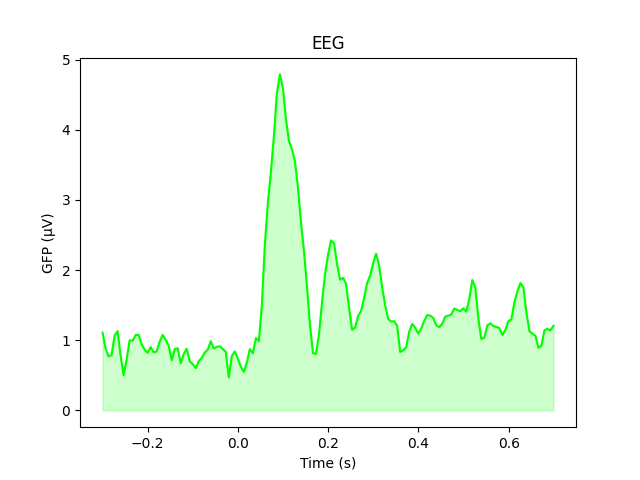
As stated above, the GFP is the population standard deviation of the signal across channels. To compute it manually, we can leverage the fact that evoked.data is a NumPy array, and verify by plotting it using matplotlib commands:

gfp = l_aud.data.std(axis=0, ddof=0)

# Reproducing the MNE-Python plot style seen above
fig, ax = plt.subplots()
ax.plot(l_aud.times, gfp * 1e6, color='lime')
ax.fill_between(l_aud.times, gfp * 1e6, color='lime', alpha=0.2)
ax.set(xlabel='Time (s)', ylabel='GFP (µV)', title='EEG')

Analyzing regions of interest (ROIs): averaging across channels

Since our sample data is responses to left and right auditory and visual stimuli, we may want to compare left versus right ROIs. To average across channels in a region of interest, we first find the channel indices we want. Looking back at the 2D sensor plot above, we might choose the following for left and right ROIs:

left = ['eeg17', 'eeg18', 'eeg25', 'eeg26']
right = ['eeg23', 'eeg24', 'eeg34', 'eeg35']

left_ix = mne.pick_channels(l_aud.info['ch_names'], include=left)
right_ix = mne.pick_channels(l_aud.info['ch_names'], include=right)

Now we can create a new Evoked with 2 virtual channels (one for each ROI):

roi_dict = dict(left_ROI=left_ix, right_ROI=right_ix)
roi_evoked = mne.channels.combine_channels(l_aud, roi_dict, method='mean')
print(roi_evoked.info['ch_names'])
roi_evoked.plot()

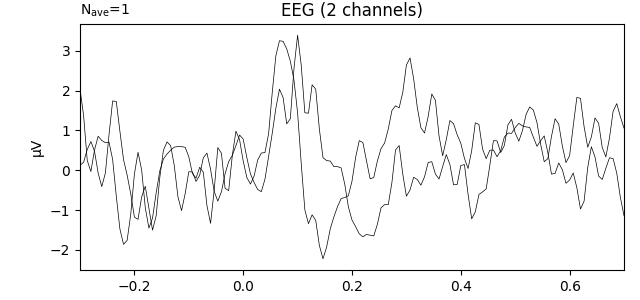
Out:

['left_ROI', 'right_ROI']

Comparing conditions

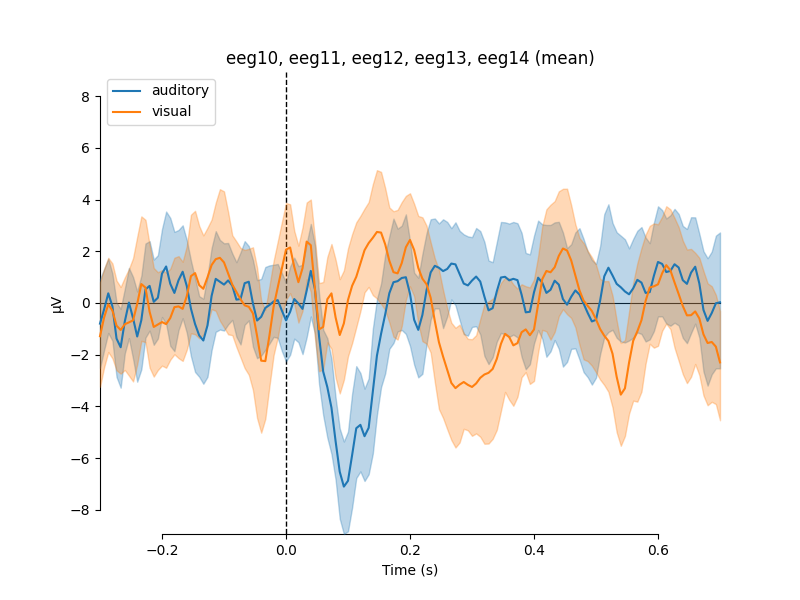
If we wanted to compare our auditory and visual stimuli, a useful function is mne.viz.plot_compare_evokeds. By default this will combine all channels in each evoked object using global field power (or RMS for MEG channels); here instead we specify to combine by averaging, and restrict it to a subset of channels by passing picks:

evokeds = dict(auditory=l_aud, visual=l_vis)
picks = [f'eeg{n}' for n in range(10, 15)]
mne.viz.plot_compare_evokeds(evokeds, picks=picks, combine='mean')

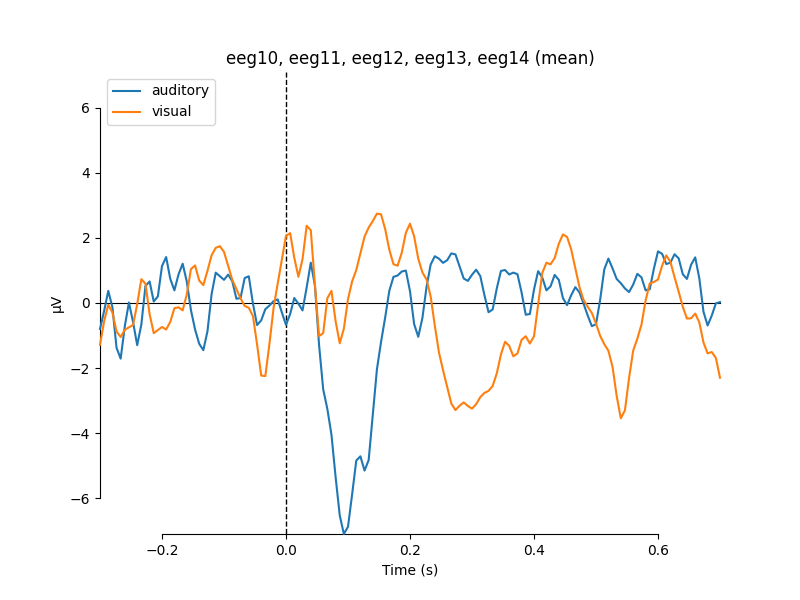
Out:

combining channels using "mean"
combining channels using "mean"

We can also easily get confidence intervals by treating each epoch as a separate observation using the iter_evoked method. A confidence interval across subjects could also be obtained, by passing a list of Evoked objects (one per subject) to the plot_compare_evokeds function.

evokeds = dict(auditory=list(epochs['auditory/left'].iter_evoked()),
               visual=list(epochs['visual/left'].iter_evoked()))
mne.viz.plot_compare_evokeds(evokeds, combine='mean', picks=picks)

Out:

combining channels using "mean"
combining channels using "mean"

We can also compare conditions by subtracting one Evoked object from another using the mne.combine_evoked function (this function also allows pooling of epochs without subtraction).

aud_minus_vis = mne.combine_evoked([l_aud, l_vis], weights=[1, -1])
aud_minus_vis.plot_joint()

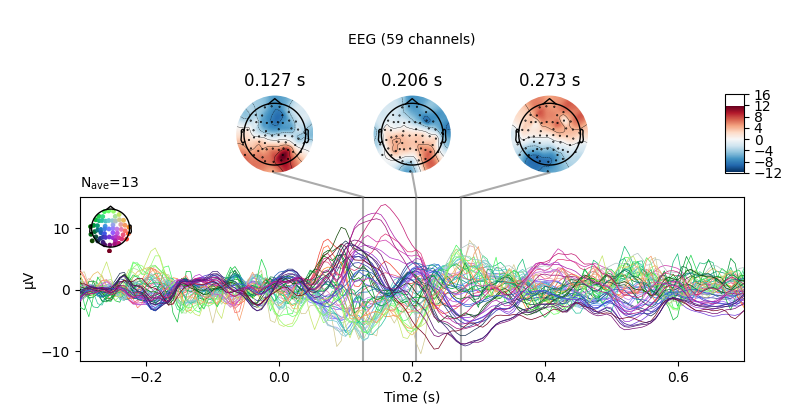
Out:

Projections have already been applied. Setting proj attribute to True.

Warning

The code above yields an equal-weighted difference. If you have imbalanced trial numbers, you might want to equalize the number of events per condition first by using epochs.equalize_event_counts() before averaging.

Grand averages

To compute grand averages across conditions (or subjects), you can pass a list of Evoked objects to mne.grand_average. The result is another Evoked object.

grand_average = mne.grand_average([l_aud, l_vis])
print(grand_average)

Out:

Interpolating bad channels
    Automatic origin fit: head of radius 91.0 mm
Computing interpolation matrix from 59 sensor positions
Interpolating 1 sensors
Interpolating bad channels
    Automatic origin fit: head of radius 91.0 mm
Computing interpolation matrix from 59 sensor positions
Interpolating 1 sensors
Identifying common channels ...
<Evoked | 'Grand average (n = 2)' (average, N=2), -0.29969 – 0.69928 sec, baseline -0.299693 – 0 sec, 60 ch, ~3.0 MB>

For combining conditions it is also possible to make use of HED tags in the condition names when selecting which epochs to average. For example, we have the condition names:

list(event_dict)

We can select the auditory conditions (left and right together) by passing:

epochs['auditory'].average()

see Subselecting epochs for details.

The tutorials The Epochs data structure: discontinuous data and The Evoked data structure: evoked/averaged data have many more details about working with the Epochs and Evoked classes.

Amplitude and latency measures

It is common in ERP research to extract measures of amplitude or latency to compare across different conditions. There are many measures that can be extracted from ERPs, and many of these are detailed (including the respective strengths and weaknesses) in chapter 9 of Luck 4 (also see the Measurement Tool in the ERPLAB Toolbox 5).

This part of the tutorial will demonstrate how to extract three common measures:

• Peak latency

• Peak amplitude

• Mean amplitude

Peak latency and amplitude

The most common measures of amplitude and latency are peak measures. Peak measures are basically the maximum amplitude of the signal in a specified time window and the time point (or latency) at which the peak amplitude occurred.

Peak measures can be obtained using the get_peak() method. There are two important things to point out about get_peak() method. First, it finds the strongest peak looking across all channels of the selected type that are available in the Evoked object. As a consequence, if you want to restrict the search for the peak to a group of channels or a single channel, you should first use the pick() or pick_channels() methods. Second, the get_peak() method can find different types of peaks using the mode argument. There are three options:

• mode='pos': finds the peak with a positive voltage (ignores negative voltages)

• mode='neg': finds the peak with a negative voltage (ignores positive voltages)

• mode='abs': finds the peak with the largest absolute voltage regardless of sign (positive or negative)

The following example demonstrates how to find the first positive peak in the ERP (i.e., the P100) for the left visual condition (i.e., the l_vis Evoked object). The time window used to search for the peak ranges from .08 to .12 s. This time window was selected because it is when P100 typically occurs. Note that all 'eeg' channels are submitted to the get_peak() method.

# Define a function to print out the channel (ch) containing the
# peak latency (lat; in msec) and amplitude (amp, in µV), with the
# time range (tmin and tmax) that were searched.
# This function will be used throughout the remainder of the tutorial
def print_peak_measures(ch, tmin, tmax, lat, amp):
    print(f'Channel: {ch}')
    print(f'Time Window: {tmin * 1e3:.3f} - {tmax * 1e3:.3f} ms')
    print(f'Peak Latency: {lat * 1e3:.3f} ms')
    print(f'Peak Amplitude: {amp * 1e6:.3f} µV')


# Get peak amplitude and latency from a good time window that contains the peak
good_tmin, good_tmax = .08, .12
ch, lat, amp = l_vis.get_peak(ch_type='eeg', tmin=good_tmin, tmax=good_tmax,
                              mode='pos', return_amplitude=True)

# Print output from the good time window that contains the peak
print('** PEAK MEASURES FROM A GOOD TIME WINDOW **')
print_peak_measures(ch, good_tmin, good_tmax, lat, amp)

Out:

** PEAK MEASURES FROM A GOOD TIME WINDOW **
Channel: eeg55
Time Window: 80.000 - 120.000 ms
Peak Latency: 86.578 ms
Peak Amplitude: 6.508 µV

The output shows that channel eeg55 had the maximum positive peak in the chosen time window from all of the 'eeg' channels searched. In practice, one might want to pull out the peak for an a priori region of interest or a single channel depending on the study. This can be done by combining the pick() or pick_channels() methods with the get_peak() method.

Here, let’s assume we believe the effects of interest will occur at eeg59.

# Fist, return a copy of l_vis to select the channel from
l_vis_roi = l_vis.copy().pick('eeg59')

# Get the peak and latency measure from the selected channel
ch_roi, lat_roi, amp_roi = l_vis_roi.get_peak(
    tmin=good_tmin, tmax=good_tmax, mode='pos', return_amplitude=True)

# Print output
print('** PEAK MEASURES FOR ONE CHANNEL FROM A GOOD TIME WINDOW **')
print_peak_measures(ch_roi, good_tmin, good_tmax, lat_roi, amp_roi)

Out:

** PEAK MEASURES FOR ONE CHANNEL FROM A GOOD TIME WINDOW **
Channel: eeg59
Time Window: 80.000 - 120.000 ms
Peak Latency: 86.578 ms
Peak Amplitude: 5.713 µV

While the peak latencies are the same in channels eeg55 and eeg59, the peak amplitudes differ. This approach can also be applied to virtual channels created with the combine_channels() function and difference waves created with the mne.combine_evoked() function (see aud_minus_vis in section Comparing conditions above).

Peak measures are very susceptible to high frequency noise in the signal (for discussion, see 4). Specifically, high frequency noise positively bias peak amplitude measures. This bias can confound comparisons across conditions where ERPs differ in the level of high frequency noise, such as when the conditions differ in the number of trials contributing to the ERP. One way to avoid this is to apply a non-causal low-pass filter to the ERP. Low-pass filters reduce the contribution of high frequency noise by smoothing out fast (i.e., high frequency) fluctuations in the signal (see Background information on filtering). While this can reduce the positive bias in peak amplitude measures caused by high frequency noise, low-pass filtering the ERP can introduce challenges in interpreting peak latency measures for effects of interest 67.

If using peak measures, it is critical to visually inspect the data to make sure the selected time window actually contains a peak (get_peak() will always identify a peak). Visual inspection allows to easily verify whether the automatically found peak is correct. The get_peak() detects the maximum or minimum voltage in the specified time range and returns the latency and amplitude of this peak. There is no guarantee that this method will return an actual peak. Instead, it may return a value on the rising or falling edge of the peak we are trying to find.

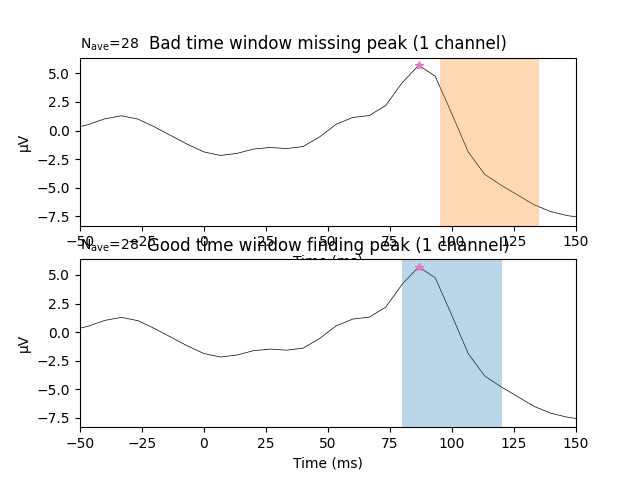
The following example demonstrates why visual inspection is crucial. Below, we use a known bad time window (.095 to .135 s) to search for a peak in channel eeg59.

# Get BAD peak measures
bad_tmin, bad_tmax = .095, .135
ch_roi, bad_lat_roi, bad_amp_roi = l_vis_roi.get_peak(
    mode='pos', tmin=bad_tmin, tmax=bad_tmax, return_amplitude=True)

# Print output
print('** PEAK MEASURES FOR ONE CHANNEL FROM A BAD TIME WINDOW **')
print_peak_measures(ch_roi, bad_tmin, bad_tmax, bad_lat_roi, bad_amp_roi)

Out:

** PEAK MEASURES FOR ONE CHANNEL FROM A BAD TIME WINDOW **
Channel: eeg59
Time Window: 95.000 - 135.000 ms
Peak Latency: 99.898 ms
Peak Amplitude: 1.487 µV

If all we had were the above values, it would be unclear if they are truly identifying a peak or just a the falling or rising edge of one. However, it becomes clear that the .095 to .135 s time window is misses the peak on eeg59. This is shown in the bottom panel where we see the bad time window (highlighted in orange) misses the peak (the pink star). In contrast, the time window defined initially (.08 to .12 s; highlighted in blue) returns an actual peak instead of a just a maximal or minimal value in the searched time window. Visual inspection will always help you to convince yourself the data returned are actual peaks.

fig, axs = plt.subplots(nrows=2, ncols=1)
words = (('Bad', 'missing'), ('Good', 'finding'))
times = (np.array([bad_tmin, bad_tmax]), np.array([good_tmin, good_tmax]))
colors = ('C1', 'C0')

for ix, ax in enumerate(axs):
    title = '{} time window {} peak'.format(*words[ix])
    l_vis_roi.plot(axes=ax, time_unit='ms', show=False, titles=title)
    ax.plot(lat_roi * 1e3, amp_roi * 1e6, marker='*', color='C6')
    ax.axvspan(*(times[ix] * 1e3), facecolor=colors[ix], alpha=0.3)
    ax.set_xlim(-50, 150)  # Show zoomed in around peak

Out:

Need more than one channel to make topography for eeg. Disabling interactivity.
Need more than one channel to make topography for eeg. Disabling interactivity.

Mean Amplitude

Another common practice in ERP studies is to define a component (or effect) as the mean amplitude within a specified time window. One advantage of this approach is that it is less sensitive to high frequency noise (compared to peak amplitude measures) because averaging over a time window acts like a low-pass filter (see discussion in the above section Peak latency and amplitude).

When using mean amplitude measures, selecting the time window based on the effect of interest (e.g., the difference between two conditions) can inflate the likelihood of finding false positives in your results because this approach is circular 8. There are other, and better, ways to identify a time window to use for extracting mean amplitude measures. First, you can use a priori time window based on prior research. A second way is to define a time window from an independent condition or set of trials not used in the analysis (e.g., a “localizer”). A third approach is to define a time window using the across-condition grand average. This latter approach is not circular because the across-condition mean and condition difference are independent of one another. The issues discussed above also apply to selecting channels used for analysis.

The following example demonstrates how to pull out the mean amplitude from the left visual condition (i.e., the l_vis Evoked object) using from selected channels and time windows. Stimulating the left visual field is increases neural activity visual cortex of the contralateral (i.e., right) hemisphere. We can test this by examining the amplitude of the ERP for left visual field stimulation over right (contralateral) and left (ipsilateral) channels. The channels used for this analysis are eeg54 and eeg57 (left hemisphere), and eeg59 and eeg55 (right hemisphere). The time window used is .08 (good_tmin) to .12 s (good_tmax) as it corresponds to when P100 typically occurs. The P100 is sensitive to left and right visual field stimulation. The mean amplitude is extracted from the above four channels and stored in a pandas.DataFrame.

# Select all of the channels and crop to the time window
channels = ['eeg54', 'eeg57', 'eeg55', 'eeg59']
hemisphere = ['left', 'left', 'right', 'right']
l_vis_mean_roi = l_vis.copy().pick(channels).crop(
    tmin=good_tmin, tmax=good_tmax)

# Extract mean amplitude in µV over time
mean_amp_roi = l_vis_mean_roi.data.mean(axis=1) * 1e6

# Store the data in a data frame
mean_amp_roi_df = pd.DataFrame({
    'ch_name': l_vis_mean_roi.ch_names,
    'hemisphere': ['left', 'left', 'right', 'right'],
    'mean_amp': mean_amp_roi
})

# Print the data frame
print(mean_amp_roi_df.groupby('hemisphere').mean())

Out:

            mean_amp
hemisphere
left       -0.279764
right       0.685840

As demonstrated in the above example, the mean amplitude was higher and positive in right compared to left hemisphere channels. It should be reiterated that both that spatial and temporal window you use should be determined in an independent manner (e.g., defined a priori from prior research, a “localizer” or another independent condition) and not based on the data you will use to test your hypotheses.

The above example can be modified to extract the the mean amplitude from all channels and store the resulting output in pandas.DataFrame. This can be useful for statistical analyses conducted in other programming languages.

# Extract mean amplitude for all channels in l_vis (including `eog`)
l_vis_cropped = l_vis.copy().crop(tmin=good_tmin, tmax=good_tmax)
mean_amp_all = l_vis_cropped.data.mean(axis=1) * 1e6
mean_amp_all_df = pd.DataFrame({
    'ch_name': l_vis_cropped.info['ch_names'],
    'mean_amp': mean_amp_all
})
mean_amp_all_df['tmin'] = good_tmin
mean_amp_all_df['tmax'] = good_tmax
mean_amp_all_df['condition'] = 'Left/Visual'
print(mean_amp_all_df.head())
print(mean_amp_all_df.tail())

Out:

  ch_name  ...    condition
0   eeg01  ...  Left/Visual
1   eeg02  ...  Left/Visual
2   eeg03  ...  Left/Visual
3   eeg04  ...  Left/Visual
4   eeg05  ...  Left/Visual

[5 rows x 5 columns]
   ch_name  ...    condition
55   eeg56  ...  Left/Visual
56   eeg57  ...  Left/Visual
57   eeg58  ...  Left/Visual
58   eeg59  ...  Left/Visual
59   eeg60  ...  Left/Visual

[5 rows x 5 columns]

References

1

Dietrich Lehmann and Wolfgang Skrandies. Reference-free identification of components of checkerboard-evoked multichannel potential fields. Electroencephalography and Clinical Neurophysiology, 48(6):609–621, 1980. doi:10.1016/0013-4694(80)90419-8.

2

Dietrich Lehmann and Wolfgang Skrandies. Spatial analysis of evoked potentials in man—a review. Progress in Neurobiology, 23(3):227–250, 1984. doi:10.1016/0301-0082(84)90003-0.

3

Micah M. Murray, Denis Brunet, and Christoph M. Michel. Topographic ERP analyses: A step-by-step tutorial review. Brain Topography, 20(4):249–264, 2008. doi:10.1007/s10548-008-0054-5.

4(1,2)

Steven J Luck. An Introduction to the Event-Related Potential Technique. The MIT Press, Cambridge, MA, 2nd edition, 2014. ISBN 978-0-262-52585-5. URL: https://mitpress.mit.edu/books/introduction-event-related-potential-technique-second-edition.

5

Javier Lopez-Calderon and Steven J. Luck. Erplab: an open-source toolbox for the analysis of event-related potentials. Frontiers in Human Neuroscience, 2014. doi:10.3389/fnhum.2014.00213.

6

Guillaume A. Rousselet. Does filtering preclude us from studying ERP time-courses? Frontiers in Psychology, 2012. doi:10.3389/fpsyg.2012.00131.

7

Rufin VanRullen. Four common conceptual fallacies in mapping the time course of recognition. Frontiers in Psychology, 2011. doi:10.3389/fpsyg.2011.00365.

8

Steven J. Luck and Nicholas Gaspelin. How to get statistically significant effects in any ERP experiment (and why you shouldn’t). Psychophysiology, 54(1):146–157, 2017. doi:10.1111/psyp.12639.

Estimated memory usage: 9 MB

previous

Visualizing Evoked data

next

Plotting whitened data