Note
Click here to download the full example code
Plotting the full vector-valued MNE solution¶
The source space that is used for the inverse computation defines a set of
dipoles, distributed across the cortex. When visualizing a source estimate, it
is sometimes useful to show the dipole directions in addition to their
estimated magnitude. This can be accomplished by computing a
mne.VectorSourceEstimate and plotting it with
stc.plot, which uses
plot_vector_source_estimates() under the hood rather than
plot_source_estimates().
It can also be instructive to visualize the actual dipole/activation locations
in 3D space in a glass brain, as opposed to activations imposed on an inflated
surface (as typically done in mne.SourceEstimate.plot()), as it allows
you to get a better sense of the underlying source geometry.
# Author: Marijn van Vliet <w.m.vanvliet@gmail.com>
#
# License: BSD-3-Clause
import numpy as np
import mne
from mne.datasets import sample
from mne.minimum_norm import read_inverse_operator, apply_inverse
print(__doc__)
data_path = sample.data_path()
subjects_dir = data_path + '/subjects'
smoothing_steps = 7
# Read evoked data
fname_evoked = data_path + '/MEG/sample/sample_audvis-ave.fif'
evoked = mne.read_evokeds(fname_evoked, condition=0, baseline=(None, 0))
# Read inverse solution
fname_inv = data_path + '/MEG/sample/sample_audvis-meg-oct-6-meg-inv.fif'
inv = read_inverse_operator(fname_inv)
# Apply inverse solution, set pick_ori='vector' to obtain a
# :class:`mne.VectorSourceEstimate` object
snr = 3.0
lambda2 = 1.0 / snr ** 2
stc = apply_inverse(evoked, inv, lambda2, 'dSPM', pick_ori='vector')
# Use peak getter to move visualization to the time point of the peak magnitude
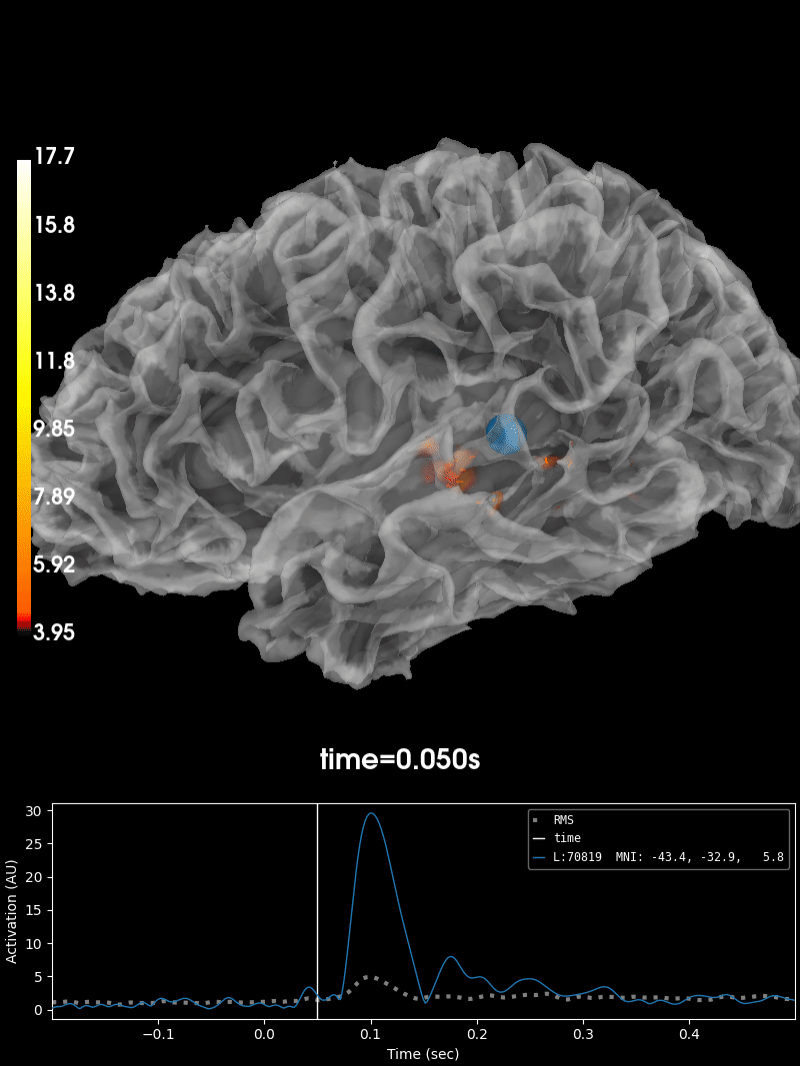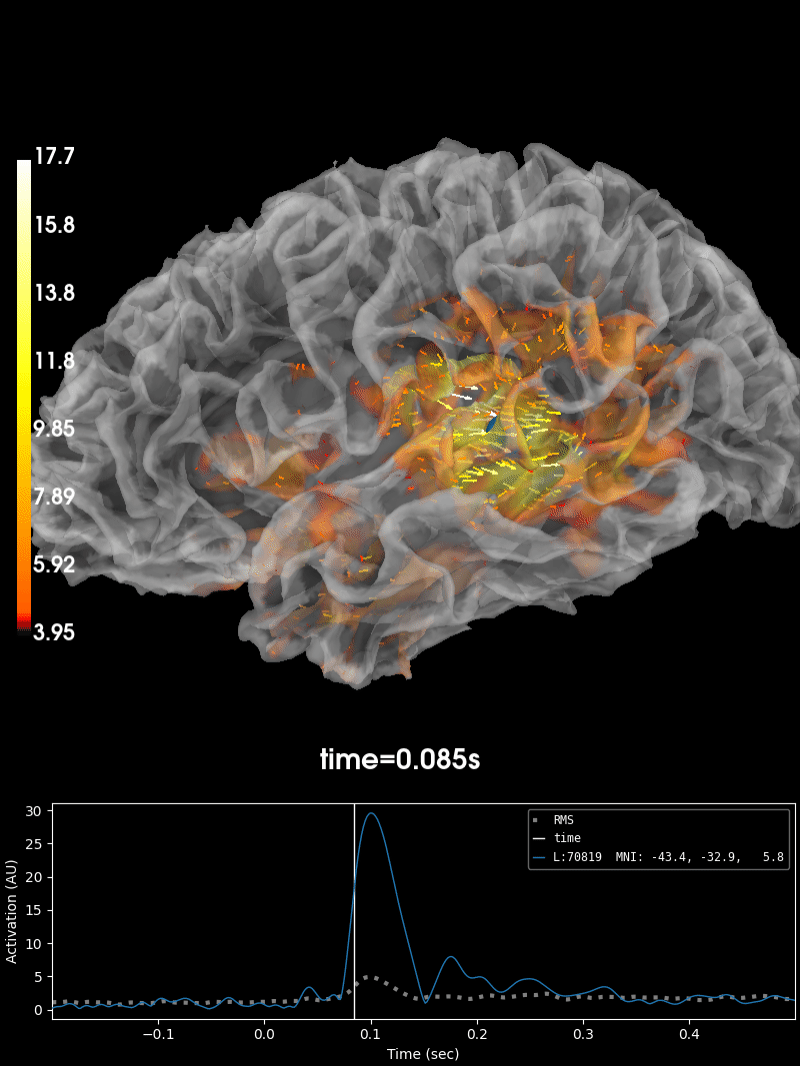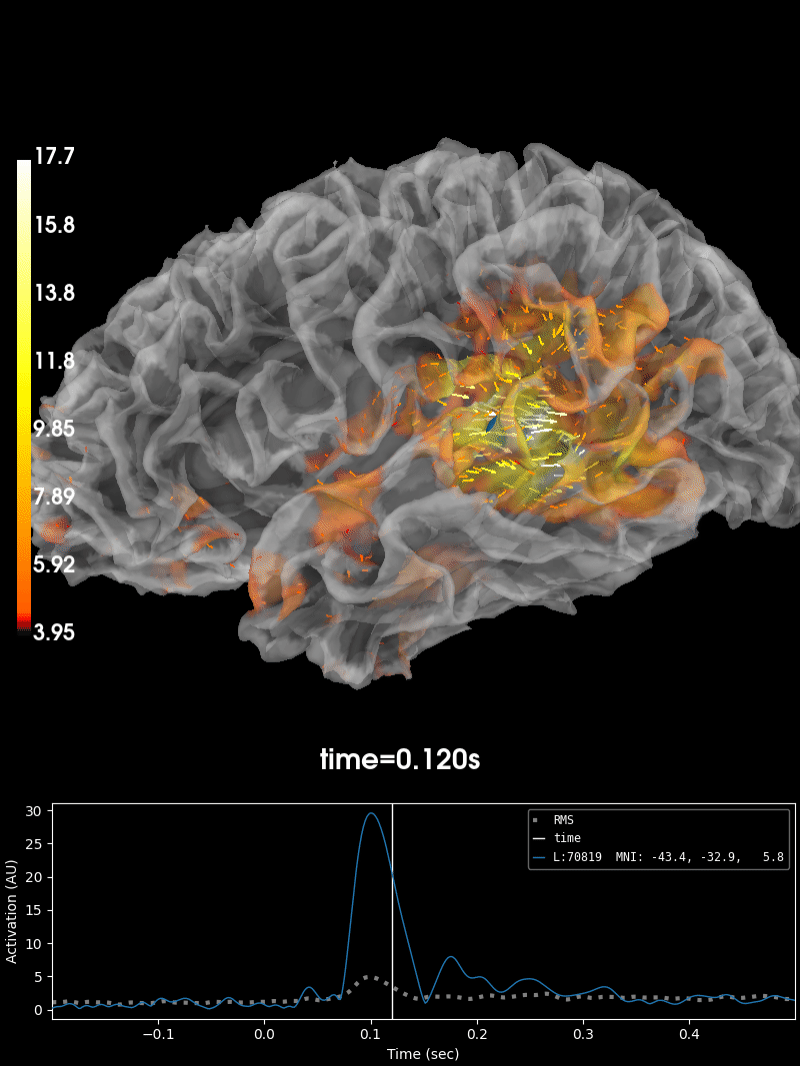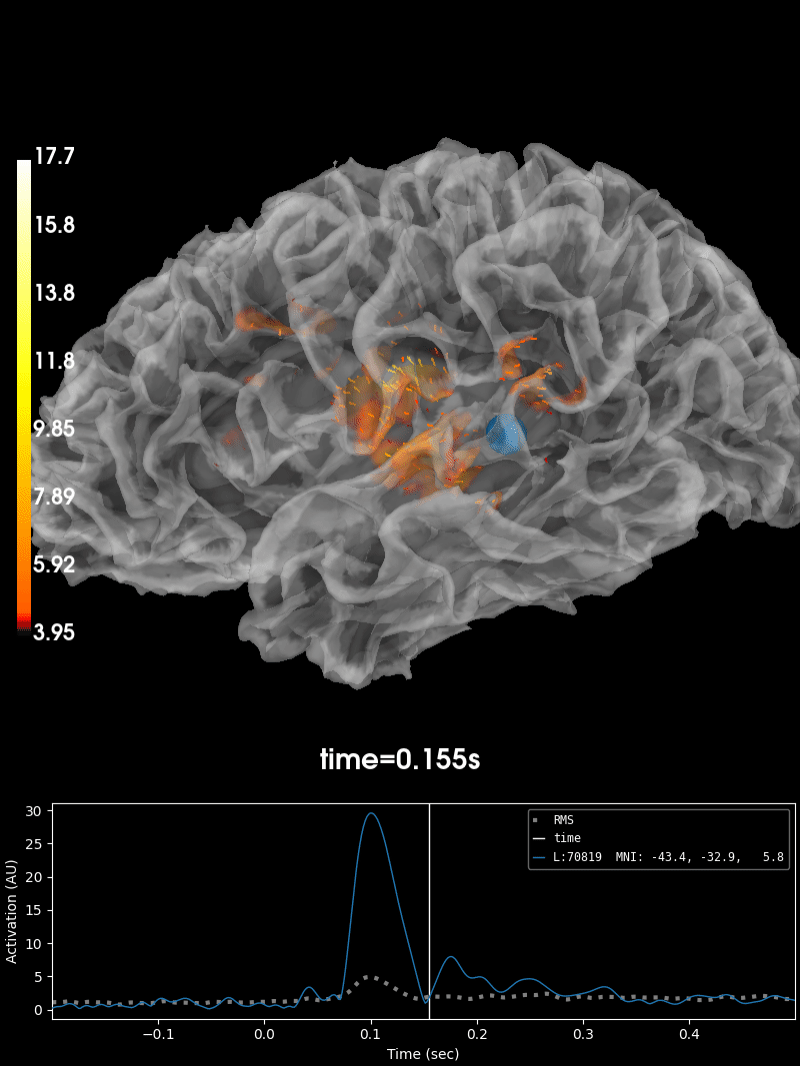
_, peak_time = stc.magnitude().get_peak(hemi='lh')
Out:
Reading /home/circleci/mne_data/MNE-sample-data/MEG/sample/sample_audvis-ave.fif ...
Read a total of 4 projection items:
PCA-v1 (1 x 102) active
PCA-v2 (1 x 102) active
PCA-v3 (1 x 102) active
Average EEG reference (1 x 60) active
Found the data of interest:
t = -199.80 ... 499.49 ms (Left Auditory)
0 CTF compensation matrices available
nave = 55 - aspect type = 100
Projections have already been applied. Setting proj attribute to True.
Applying baseline correction (mode: mean)
Reading inverse operator decomposition from /home/circleci/mne_data/MNE-sample-data/MEG/sample/sample_audvis-meg-oct-6-meg-inv.fif...
Reading inverse operator info...
[done]
Reading inverse operator decomposition...
[done]
305 x 305 full covariance (kind = 1) found.
Read a total of 4 projection items:
PCA-v1 (1 x 102) active
PCA-v2 (1 x 102) active
PCA-v3 (1 x 102) active
Average EEG reference (1 x 60) active
Noise covariance matrix read.
22494 x 22494 diagonal covariance (kind = 2) found.
Source covariance matrix read.
22494 x 22494 diagonal covariance (kind = 6) found.
Orientation priors read.
22494 x 22494 diagonal covariance (kind = 5) found.
Depth priors read.
Did not find the desired covariance matrix (kind = 3)
Reading a source space...
Computing patch statistics...
Patch information added...
Distance information added...
[done]
Reading a source space...
Computing patch statistics...
Patch information added...
Distance information added...
[done]
2 source spaces read
Read a total of 4 projection items:
PCA-v1 (1 x 102) active
PCA-v2 (1 x 102) active
PCA-v3 (1 x 102) active
Average EEG reference (1 x 60) active
Source spaces transformed to the inverse solution coordinate frame
Preparing the inverse operator for use...
Scaled noise and source covariance from nave = 1 to nave = 55
Created the regularized inverter
Created an SSP operator (subspace dimension = 3)
Created the whitener using a noise covariance matrix with rank 302 (3 small eigenvalues omitted)
Computing noise-normalization factors (dSPM)...
[done]
Applying inverse operator to "Left Auditory"...
Picked 305 channels from the data
Computing inverse...
Eigenleads need to be weighted ...
Computing residual...
Explained 59.4% variance
dSPM...
[done]
Plot the source estimate:
brain = stc.plot(
initial_time=peak_time, hemi='lh', subjects_dir=subjects_dir,
smoothing_steps=smoothing_steps)
# You can save a brain movie with:
# brain.save_movie(time_dilation=20, tmin=0.05, tmax=0.16, framerate=10,
# interpolation='linear', time_viewer=True)