Note
Go to the end to download the full example code.
XDAWN Decoding From EEG data#
ERP decoding with Xdawn [1][2]. For each event type, a set of spatial Xdawn filters are trained and applied on the signal. Channels are concatenated and rescaled to create features vectors that will be fed into a logistic regression.
# Authors: Alexandre Barachant <alexandre.barachant@gmail.com>
#
# License: BSD-3-Clause
# Copyright the MNE-Python contributors.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.model_selection import StratifiedKFold
from sklearn.multiclass import OneVsRestClassifier
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import MinMaxScaler
from mne import Epochs, io, pick_types, read_events
from mne.datasets import sample
from mne.decoding import Vectorizer, XdawnTransformer, get_spatial_filter_from_estimator
from mne.utils import check_version
print(__doc__)
data_path = sample.data_path()
Set parameters and read data
meg_path = data_path / "MEG" / "sample"
raw_fname = meg_path / "sample_audvis_filt-0-40_raw.fif"
event_fname = meg_path / "sample_audvis_filt-0-40_raw-eve.fif"
tmin, tmax = -0.1, 0.3
event_id = {
"Auditory/Left": 1,
"Auditory/Right": 2,
"Visual/Left": 3,
"Visual/Right": 4,
}
n_filter = 3
# Setup for reading the raw data
raw = io.read_raw_fif(raw_fname, preload=True)
raw.filter(1, 20, fir_design="firwin")
events = read_events(event_fname)
picks = pick_types(raw.info, meg=False, eeg=True, stim=False, eog=False, exclude="bads")
epochs = Epochs(
raw,
events,
event_id,
tmin,
tmax,
proj=False,
picks=picks,
baseline=None,
preload=True,
verbose=False,
)
# Create classification pipeline
kwargs = dict()
if check_version("sklearn", "1.8"):
kwargs["l1_ratio"] = 1
else:
kwargs["penalty"] = "l1"
clf = make_pipeline(
XdawnTransformer(n_components=n_filter),
Vectorizer(),
MinMaxScaler(),
OneVsRestClassifier(LogisticRegression(solver="liblinear", **kwargs)),
)
# Get the data and labels
# X is of shape (n_epochs, n_channels, n_times)
X = epochs.get_data(copy=False)
y = epochs.events[:, -1]
# Cross validator
cv = StratifiedKFold(n_splits=10, shuffle=True, random_state=42)
# Do cross-validation
preds = np.empty(len(y))
for train, test in cv.split(epochs, y):
clf.fit(X[train], y[train])
preds[test] = clf.predict(X[test])
# Classification report
target_names = ["aud_l", "aud_r", "vis_l", "vis_r"]
report = classification_report(y, preds, target_names=target_names)
print(report)
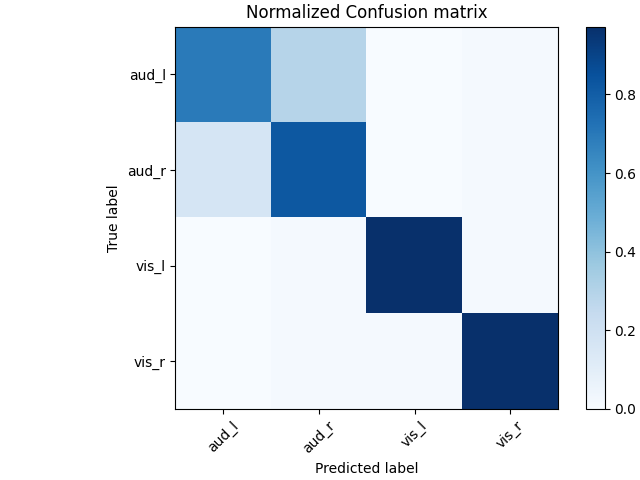
# Normalized confusion matrix
cm = confusion_matrix(y, preds)
cm_normalized = cm.astype(float) / cm.sum(axis=1)[:, np.newaxis]
# Plot confusion matrix
fig, ax = plt.subplots(1, layout="constrained")
im = ax.imshow(cm_normalized, interpolation="nearest", cmap=plt.cm.Blues)
ax.set(title="Normalized Confusion matrix")
fig.colorbar(im)
tick_marks = np.arange(len(target_names))
plt.xticks(tick_marks, target_names, rotation=45)
plt.yticks(tick_marks, target_names)
ax.set(ylabel="True label", xlabel="Predicted label")
Opening raw data file /home/circleci/mne_data/MNE-sample-data/MEG/sample/sample_audvis_filt-0-40_raw.fif...
Read a total of 4 projection items:
PCA-v1 (1 x 102) idle
PCA-v2 (1 x 102) idle
PCA-v3 (1 x 102) idle
Average EEG reference (1 x 60) idle
Range : 6450 ... 48149 = 42.956 ... 320.665 secs
Ready.
Reading 0 ... 41699 = 0.000 ... 277.709 secs...
Filtering raw data in 1 contiguous segment
Setting up band-pass filter from 1 - 20 Hz
FIR filter parameters
---------------------
Designing a one-pass, zero-phase, non-causal bandpass filter:
- Windowed time-domain design (firwin) method
- Hamming window with 0.0194 passband ripple and 53 dB stopband attenuation
- Lower passband edge: 1.00
- Lower transition bandwidth: 1.00 Hz (-6 dB cutoff frequency: 0.50 Hz)
- Upper passband edge: 20.00 Hz
- Upper transition bandwidth: 5.00 Hz (-6 dB cutoff frequency: 22.50 Hz)
- Filter length: 497 samples (3.310 s)
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Computing rank from data with rank='full'
data: rank 59 from info
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Computing rank from data with rank='full'
data: rank 59 from info
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Computing rank from data with rank='full'
data: rank 59 from info
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Computing rank from data with rank='full'
data: rank 59 from info
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Computing rank from data with rank='full'
data: rank 59 from info
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Computing rank from data with rank='full'
data: rank 59 from info
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Computing rank from data with rank='full'
data: rank 59 from info
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Computing rank from data with rank='full'
data: rank 59 from info
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Computing rank from data with rank='full'
data: rank 59 from info
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Estimating covariance using EMPIRICAL
Done.
Computing rank from data with rank='full'
data: rank 59 from info
precision recall f1-score support
aud_l 0.82 0.71 0.76 72
aud_r 0.73 0.84 0.78 73
vis_l 0.99 0.97 0.98 73
vis_r 0.96 0.97 0.96 70
accuracy 0.87 288
macro avg 0.88 0.87 0.87 288
weighted avg 0.87 0.87 0.87 288
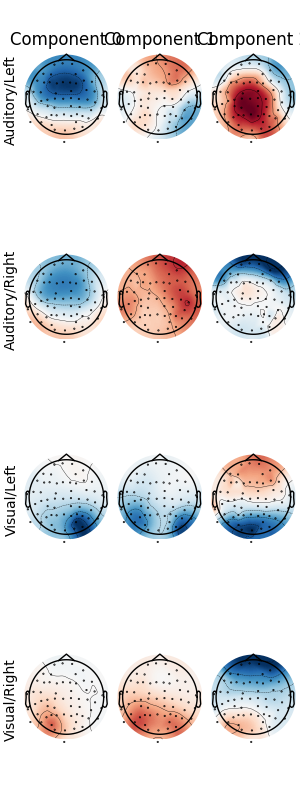
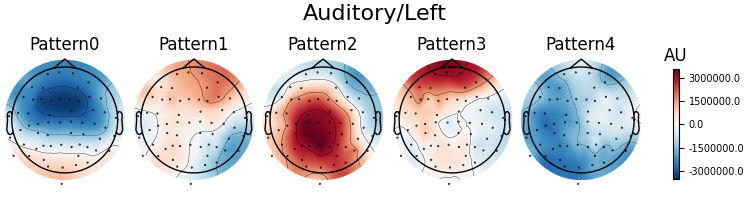
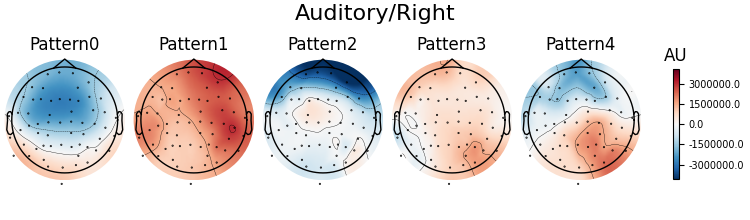
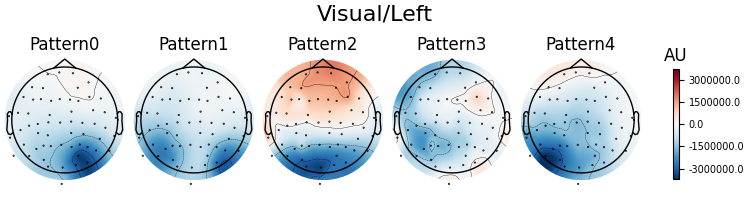
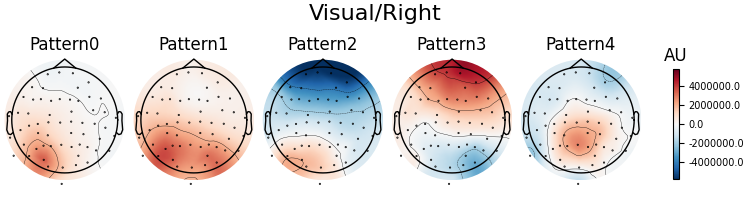
Patterns of a fitted XdawnTransformer instance (here from the last cross-validation fold) can be visualized using SpatialFilter container.
# Instantiate SpatialFilter
spf = get_spatial_filter_from_estimator(
clf, info=epochs.info, step_name="xdawntransformer"
)
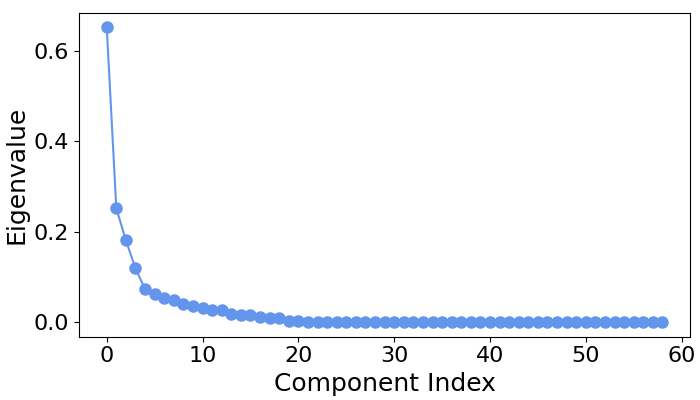
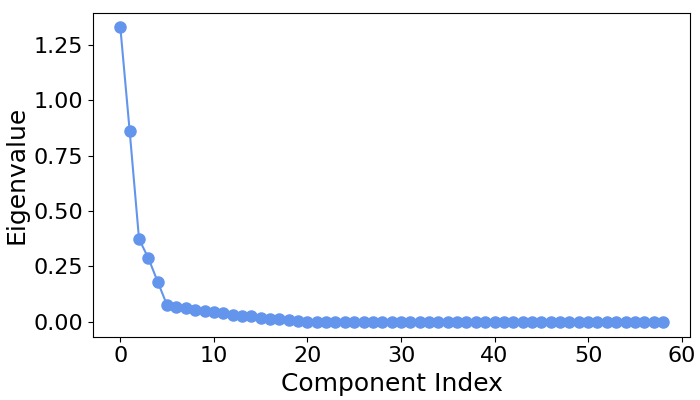
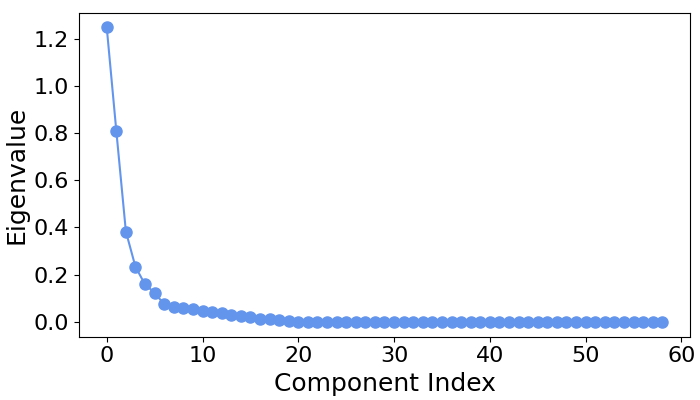
# Let's first examine the scree plot of generalized eigenvalues
# for each class.
spf.plot_scree(title="")
# We can see that for all four classes ~five largest components
# capture most of the variance, let's plot their patterns.
# Each class will now return its own figure
components_to_plot = np.arange(5)
figs = spf.plot_patterns(
# Indices of patterns to plot,
# we will plot the first three for each class
components=components_to_plot,
show=False, # to set the titles below
)
# Set the class titles
event_id_reversed = {v: k for k, v in event_id.items()}
for fig, class_idx in zip(figs, clf[0].classes_):
class_name = event_id_reversed[class_idx]
fig.suptitle(class_name, fontsize=16)
References#
Total running time of the script: (0 minutes 9.053 seconds)