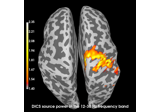
mne.beamformer.make_dics#
- mne.beamformer.make_dics(info, forward, csd, reg=0.05, noise_csd=None, label=None, pick_ori=None, rank=None, weight_norm=None, reduce_rank=False, depth=1.0, real_filter=True, inversion='matrix', verbose=None)[source]#
Compute a Dynamic Imaging of Coherent Sources (DICS) spatial filter.
This is a beamformer filter that can be used to estimate the source power at a specific frequency range [1]. It does this by constructing a spatial filter for each source point. The computation of these filters is very similar to those of the LCMV beamformer (
make_lcmv()), but instead of operating on a covariance matrix, the CSD matrix is used. When applying these filters to a CSD matrix (seeapply_dics_csd()), the source power can be estimated for each source point.- Parameters:
- info
mne.Info The
mne.Infoobject with information about the sensors and methods of measurement.- forwardinstance of
Forward Forward operator.
- csdinstance of
CrossSpectralDensity The data cross-spectral density (CSD) matrices. A source estimate is performed for each frequency or frequency-bin defined in the CSD object.
- reg
float The regularization to apply to the cross-spectral density before computing the inverse.
- noise_csdinstance of
CrossSpectralDensity|None Noise cross-spectral density (CSD) matrices. If provided, whitening will be done. The noise CSDs need to have been computed for the same frequencies as the data CSDs. Providing noise CSDs is mandatory if you mix sensor types, e.g. gradiometers with magnetometers or EEG with MEG.
New in v0.20.
- label
Label|None Restricts the solution to a given label.
- pick_ori
None|str For forward solutions with fixed orientation, None (default) must be used and a scalar beamformer is computed. For free-orientation forward solutions, a vector beamformer is computed and:
NoneOrientations are pooled after computing a vector beamformer (Default).
'normal'Filters are computed for the orientation tangential to the cortical surface.
'max-power'Filters are computed for the orientation that maximizes power.
- rank
None| ‘info’ | ‘full’ |dict This controls the rank computation that can be read from the measurement info or estimated from the data. When a noise covariance is used for whitening, this should reflect the rank of that covariance, otherwise amplification of noise components can occur in whitening (e.g., often during source localization).
NoneThe rank will be estimated from the data after proper scaling of different channel types.
'info'The rank is inferred from
info. If data have been processed with Maxwell filtering, the Maxwell filtering header is used. Otherwise, the channel counts themselves are used. In both cases, the number of projectors is subtracted from the (effective) number of channels in the data. For example, if Maxwell filtering reduces the rank to 68, with two projectors the returned value will be 66.'full'The rank is assumed to be full, i.e. equal to the number of good channels. If a
Covarianceis passed, this can make sense if it has been (possibly improperly) regularized without taking into account the true data rank.dictCalculate the rank only for a subset of channel types, and explicitly specify the rank for the remaining channel types. This can be extremely useful if you already know the rank of (part of) your data, for instance in case you have calculated it earlier.
This parameter must be a dictionary whose keys correspond to channel types in the data (e.g.
'meg','mag','grad','eeg'), and whose values are integers representing the respective ranks. For example,{'mag': 90, 'eeg': 45}will assume a rank of90and45for magnetometer data and EEG data, respectively.The ranks for all channel types present in the data, but not specified in the dictionary will be estimated empirically. That is, if you passed a dataset containing magnetometer, gradiometer, and EEG data together with the dictionary from the previous example, only the gradiometer rank would be determined, while the specified magnetometer and EEG ranks would be taken for granted.
The default is
None.New in v0.17.
- weight_norm
str|None Can be:
NoneThe unit-gain LCMV beamformer [2] will be computed.
'unit-noise-gain'The unit-noise gain minimum variance beamformer will be computed (Borgiotti-Kaplan beamformer) [2], which is not rotation invariant when
pick_ori='vector'. This should be combined withstc.project('pca')to follow the definition in [2].
'nai'The Neural Activity Index [3] will be computed, which simply scales all values from
'unit-noise-gain'by a fixed value.
'unit-noise-gain-invariant'Compute a rotation-invariant normalization using the matrix square root. This differs from
'unit-noise-gain'only whenpick_ori='vector', creating a solution that:Is rotation invariant (
'unit-noise-gain'is not);Satisfies the first requirement from [2] that
w @ w.conj().T == I, whereas'unit-noise-gain'has non-zero off-diagonals; butDoes not satisfy the second requirement that
w @ G.T = θI, which arguably does not make sense for a rotation-invariant solution.
Defaults to
None, in which case no normalization is performed.- reduce_rankbool
If True, the rank of the denominator of the beamformer formula (i.e., during pseudo-inversion) will be reduced by one for each spatial location. Setting
reduce_rank=Trueis typically necessary if you use a single sphere model with MEG data.Changed in version 0.20: Support for reducing rank in all modes (previously only supported
pick='max_power'with weight normalization).- depth
None|float|dict How to weight (or normalize) the forward using a depth prior. If float (default 0.8), it acts as the depth weighting exponent (
exp) to use None is equivalent to 0, meaning no depth weighting is performed. It can also be adictcontaining keyword arguments to pass tomne.forward.compute_depth_prior()(see docstring for details and defaults). This is effectively ignored whenmethod='eLORETA'.Changed in version 0.20: Depth bias ignored for
method='eLORETA'.- real_filterbool
If
True, take only the real part of the cross-spectral-density matrices to compute real filters.Changed in version 0.23: Version 0.23 an earlier used
real_filter=Falseas the default, as of version 0.24Trueis the default.- inversion‘single’ | ‘matrix’
This determines how the beamformer deals with source spaces in “free” orientation. Such source spaces define three orthogonal dipoles at each source point. When
inversion='single', each dipole is considered as an individual source and the corresponding spatial filter is computed for each dipole separately. Wheninversion='matrix', all three dipoles at a source vertex are considered as a group and the spatial filters are computed jointly using a matrix inversion. Whileinversion='single'is more stable,inversion='matrix'is more precise. See section 5 of [4]. Defaults to'matrix'.Changed in version 0.21: Default changed to
'matrix'.- verbosebool |
str|int|None Control verbosity of the logging output. If
None, use the default verbosity level. See the logging documentation andmne.verbose()for details. Should only be passed as a keyword argument.
- info
- Returns:
- filtersinstance of
Beamformer Dictionary containing filter weights from DICS beamformer. Contains the following keys:
- ‘kind’str
The type of beamformer, in this case ‘DICS’.
- ‘weights’ndarray, shape (n_frequencies, n_weights)
For each frequency, the filter weights of the beamformer.
- ‘csd’instance of CrossSpectralDensity
The data cross-spectral density matrices used to compute the beamformer.
- ‘ch_names’list of str
Channels used to compute the beamformer.
- ‘proj’ndarray, shape (n_channels, n_channels)
Projections used to compute the beamformer.
- ‘vertices’list of ndarray
Vertices for which the filter weights were computed.
- ‘n_sources’int
Number of source location for which the filter weight were computed.
- ‘subject’str
The subject ID.
- ‘pick-ori’None | ‘max-power’ | ‘normal’ | ‘vector’
The orientation in which the beamformer filters were computed.
- ‘inversion’‘single’ | ‘matrix’
Whether the spatial filters were computed for each dipole separately or jointly for all dipoles at each vertex using a matrix inversion.
- ‘weight_norm’None | ‘unit-noise-gain’
The normalization of the weights.
- ‘src_type’str
Type of source space.
- ‘source_nn’ndarray, shape (n_sources, 3)
For each source location, the surface normal.
- ‘is_free_ori’bool
Whether the filter was computed in a fixed direction (pick_ori=’max-power’, pick_ori=’normal’) or not.
- ‘whitener’None | ndarray, shape (n_channels, n_channels)
Whitening matrix, provided if whitening was applied to the covariance matrix and leadfield during computation of the beamformer weights.
- ‘max-power-ori’ndarray, shape (n_sources, 3) | None
When pick_ori=’max-power’, this fields contains the estimated direction of maximum power at each source location.
- filtersinstance of
See also
Notes
The original reference is [1]. See [4] for a tutorial style paper on the topic.
The DICS beamformer is very similar to the LCMV (
make_lcmv()) beamformer and many of the parameters are shared. However,make_dics()andmake_lcmv()currently have different defaults for these parameters, which were settled on separately through extensive practical use case testing (but not necessarily exhaustive parameter space searching), and it remains to be seen how functionally interchangeable they could be.The default setting reproduce the DICS beamformer as described in [4]:
inversion='single', weight_norm=None, depth=1.
To use the
make_lcmv()defaults, use:inversion='matrix', weight_norm='unit-noise-gain-invariant', depth=None
For more information about
real_filter, see the supplemental information from [5].References
Examples using mne.beamformer.make_dics#
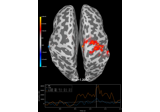
Compute source level time-frequency timecourses using a DICS beamformer
Compute evoked ERS source power using DICS, LCMV beamformer, and dSPM