mne.minimum_norm.apply_inverse#
- mne.minimum_norm.apply_inverse(evoked, inverse_operator, lambda2=0.1111111111111111, method='dSPM', pick_ori=None, prepared=False, label=None, method_params=None, return_residual=False, use_cps=True, verbose=None)[source]#
Apply inverse operator to evoked data.
- Parameters:
- evoked
Evokedobject Evoked data.
- inverse_operatorinstance of
InverseOperator Inverse operator.
- lambda2
float The regularization parameter.
- method“MNE” | “dSPM” | “sLORETA” | “eLORETA”
Use minimum norm [1], dSPM (default) [2], sLORETA [3], or eLORETA [4].
- pick_ori
None| “normal” | “vector” Options:
NonePooling is performed by taking the norm of loose/free orientations. In case of a fixed source space no norm is computed leading to signed source activity.
"normal"Only the normal to the cortical surface is kept. This is only implemented when working with loose orientations.
"vector"No pooling of the orientations is done, and the vector result will be returned in the form of a
mne.VectorSourceEstimateobject.
- preparedbool
If True, do not call
prepare_inverse_operator().- label
Label|None Restricts the source estimates to a given label. If None, source estimates will be computed for the entire source space.
- method_params
dict|None Additional options for eLORETA. See Notes for details.
New in v0.16.
- return_residualbool
If True (default False), return the residual evoked data. Cannot be used with
method=='eLORETA'.New in v0.17.
- use_cpsbool
Whether to use cortical patch statistics to define normal orientations for surfaces (default True).
Only used when the inverse is free orientation (
loose=1.), not in surface orientation, andpick_ori='normal'.New in v0.20.
- verbosebool |
str|int|None Control verbosity of the logging output. If
None, use the default verbosity level. See the logging documentation andmne.verbose()for details. Should only be passed as a keyword argument.
- evoked
- Returns:
- stc
SourceEstimate|VectorSourceEstimate|VolSourceEstimate The source estimates.
- residualinstance of
Evoked The residual evoked data, only returned if return_residual is True.
- stc
See also
apply_inverse_rawApply inverse operator to raw object.
apply_inverse_epochsApply inverse operator to epochs object.
apply_inverse_tfr_epochsApply inverse operator to epochs tfr object.
apply_inverse_covApply inverse operator to covariance object.
Notes
Currently only the
method='eLORETA'has additional options. It performs an iterative fit with a convergence criterion, so you can pass amethod_paramsdictwith string keys mapping to values for:- ‘eps’float
The convergence epsilon (default 1e-6).
- ‘max_iter’int
The maximum number of iterations (default 20). If less regularization is applied, more iterations may be necessary.
- ‘force_equal’bool
Force all eLORETA weights for each direction for a given location equal. The default is None, which means
Truefor loose-orientation inverses andFalsefor free- and fixed-orientation inverses. See below.
The eLORETA paper [4] defines how to compute inverses for fixed- and free-orientation inverses. In the free orientation case, the X/Y/Z orientation triplet for each location is effectively multiplied by a 3x3 weight matrix. This is the behavior obtained with
force_equal=Falseparameter.However, other noise normalization methods (dSPM, sLORETA) multiply all orientations for a given location by a single value. Using
force_equal=Truemimics this behavior by modifying the iterative algorithm to choose uniform weights (equivalent to a 3x3 diagonal matrix with equal entries).It is necessary to use
force_equal=Truewith loose orientation inverses (e.g.,loose=0.2), otherwise the solution resembles a free-orientation inverse (loose=1.0). It is thus recommended to useforce_equal=Truefor loose orientation andforce_equal=Falsefor free orientation inverses. This is the behavior used when the parameterforce_equal=None(default behavior).References
Examples using mne.minimum_norm.apply_inverse#

Compute MNE-dSPM inverse solution on single epochs
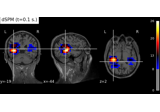
Compute MNE-dSPM inverse solution on evoked data in volume source space
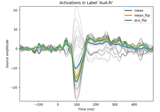
Extracting the time series of activations in a label

Compute sparse inverse solution with mixed norm: MxNE and irMxNE
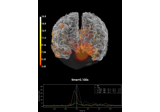
Compute MNE inverse solution on evoked data with a mixed source space

Computing source timecourses with an XFit-like multi-dipole model
Source localization with MNE, dSPM, sLORETA, and eLORETA
The role of dipole orientations in distributed source localization
EEG source localization given electrode locations on an MRI
Working with CTF data: the Brainstorm auditory dataset
Preprocessing optically pumped magnetometer (OPM) MEG data
Permutation t-test on source data with spatio-temporal clustering
Repeated measures ANOVA on source data with spatio-temporal clustering