Analysing continuous features with binning and regression in sensor space

Predict single trial activity from a continuous variable. A single-trial regression is performed in each sensor and timepoint individually, resulting in an mne.Evoked object which contains the regression coefficient (beta value) for each combination of sensor and timepoint. This example shows the regression coefficient; the t and p values are also calculated automatically.

Here, we repeat a few of the analyses from [1]. This can be easily performed by accessing the metadata object, which contains word-level information about various psycholinguistically relevant features of the words for which we have EEG activity.

For the general methodology, see e.g. [2].

# Authors: Tal Linzen <linzen@nyu.edu>
#          Denis A. Engemann <denis.engemann@gmail.com>
#          Jona Sassenhagen <jona.sassenhagen@gmail.com>
#
# License: BSD-3-Clause
# Copyright the MNE-Python contributors.

import pandas as pd

import mne
from mne.datasets import kiloword
from mne.stats import fdr_correction, linear_regression
from mne.viz import plot_compare_evokeds

# Load the data
path = kiloword.data_path() / "kword_metadata-epo.fif"
epochs = mne.read_epochs(path)
print(epochs.metadata.head())

Reading /home/circleci/mne_data/MNE-kiloword-data/kword_metadata-epo.fif ...
Isotrak not found
    Found the data of interest:
        t =    -100.00 ...     920.00 ms
        0 CTF compensation matrices available
Adding metadata with 8 columns
960 matching events found
No baseline correction applied
0 projection items activated
   WORD  Concreteness  ...  ConsonantVowelProportion  VisualComplexity
0  film          5.45  ...                      0.75         55.783710
1  cent          5.90  ...                      0.75         63.141553
2  shot          4.60  ...                      0.75         64.600033
3  cold          3.70  ...                      0.75         63.657457
4  main          3.00  ...                      0.50         68.945661

[5 rows x 8 columns]

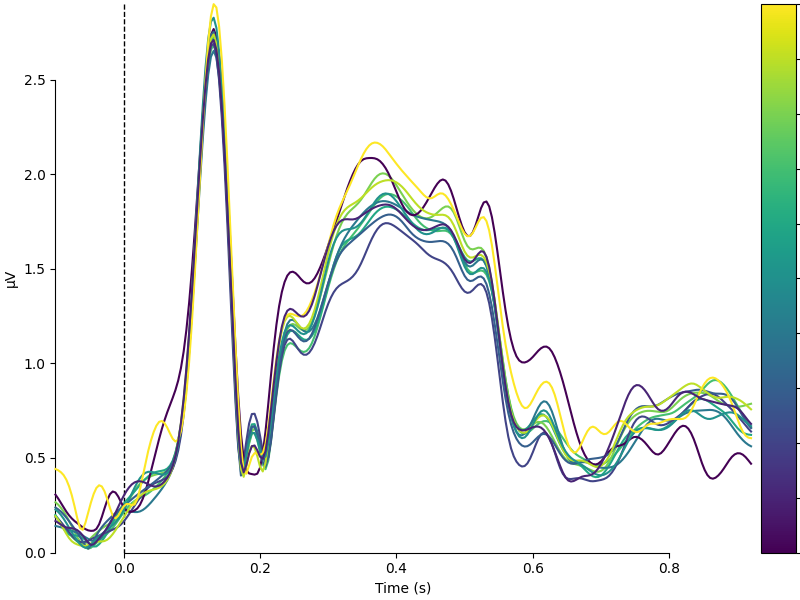
Psycholinguistically relevant word characteristics are continuous. I.e., concreteness or imaginability is a graded property. In the metadata, we have concreteness ratings on a 5-point scale. We can show the dependence of the EEG on concreteness by dividing the data into bins and plotting the mean activity per bin, color coded.

name = "Concreteness"
df = epochs.metadata
df[name] = pd.cut(df[name], 11, labels=False) / 10
colors = {str(val): val for val in df[name].unique()}
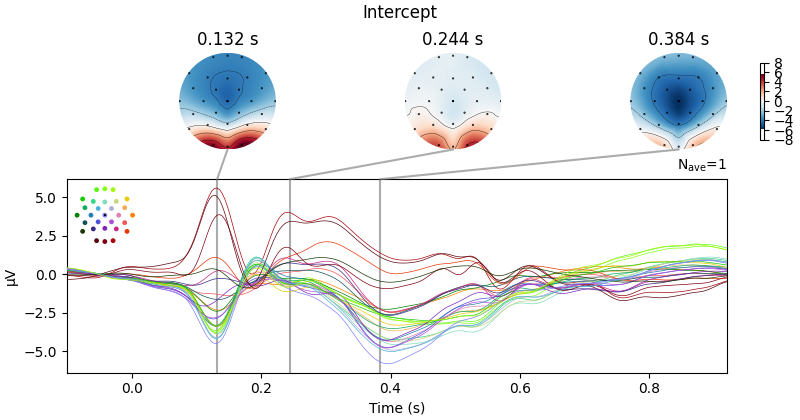
epochs.metadata = df.assign(Intercept=1)  # Add an intercept for later
evokeds = {val: epochs[name + " == " + val].average() for val in colors}
plot_compare_evokeds(
    evokeds, colors=colors, split_legend=True, cmap=(name + " Percentile", "viridis")
)

Replacing existing metadata with 9 columns
combining channels using GFP (eeg channels)
combining channels using GFP (eeg channels)
combining channels using GFP (eeg channels)
combining channels using GFP (eeg channels)
combining channels using GFP (eeg channels)
combining channels using GFP (eeg channels)
combining channels using GFP (eeg channels)
combining channels using GFP (eeg channels)
combining channels using GFP (eeg channels)
combining channels using GFP (eeg channels)
combining channels using GFP (eeg channels)

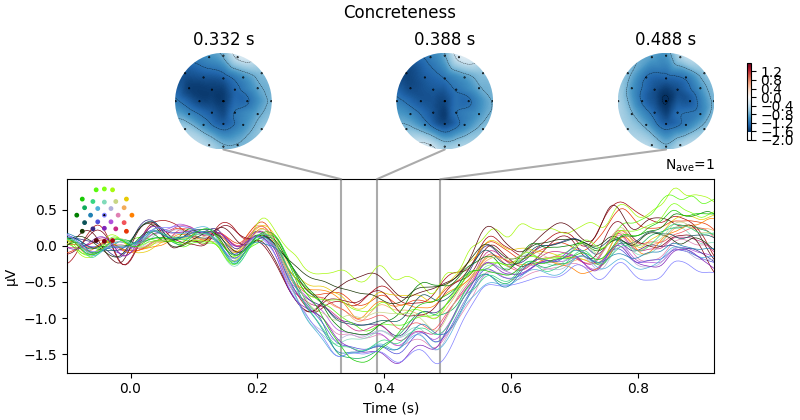
We observe that there appears to be a monotonic dependence of EEG on concreteness. We can also conduct a continuous analysis: single-trial level regression with concreteness as a continuous (although here, binned) feature. We can plot the resulting regression coefficient just like an Event-related Potential.

names = ["Intercept", name]
res = linear_regression(epochs, epochs.metadata[names], names=names)
for cond in names:
    res[cond].beta.plot_joint(
        title=cond, ts_args=dict(time_unit="s"), topomap_args=dict(time_unit="s")
    )

• 
• 

Fitting linear model to epochs, (7424 targets, 2 regressors)
Done
No projector specified for this dataset. Please consider the method self.add_proj.
No projector specified for this dataset. Please consider the method self.add_proj.

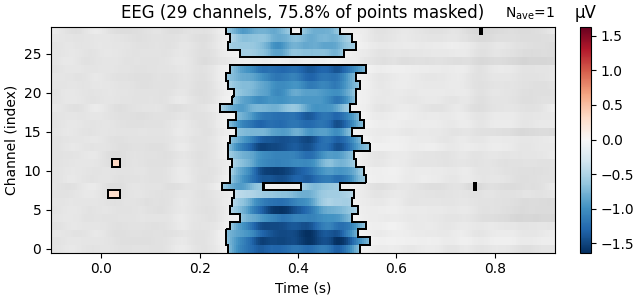
Because the linear_regression() function also estimates p values, we can – after applying FDR correction for multiple comparisons – also visualise the statistical significance of the regression of word concreteness. The mne.viz.plot_evoked_image() function takes a mask parameter. If we supply it with a boolean mask of the positions where we can reject the null hypothesis, points that are not significant will be shown transparently, and if desired, in a different colour palette and surrounded by dark contour lines.

reject_H0, fdr_pvals = fdr_correction(res["Concreteness"].p_val.data)
evoked = res["Concreteness"].beta
evoked.plot_image(mask=reject_H0, time_unit="s")

References

[1]

Stéphane Dufau, Jonathan Grainger, Katherine J. Midgley, and Phillip J. Holcomb. A thousand words are worth a picture: snapshots of printed-word processing in an event-related potential megastudy. Psychological Science, 26(12):1887–1897, 2015. doi:10.1177/0956797615603934.

[2]

Olaf Hauk, Matt H. Davis, Michael A. Ford, Friedmann Pulvermüller, and William D. Marslen-Wilson. The time course of visual word recognition as revealed by linear regression analysis of ERP data. NeuroImage, 30(4):1383–1400, 2006. doi:10.1016/j.neuroimage.2005.11.048.