Note
Go to the end to download the full example code.
How MNE uses FreeSurfer’s outputs#
This tutorial explains how MRI coordinate frames are handled in MNE-Python, and how MNE-Python integrates with FreeSurfer for handling MRI data and source space data in general.
As usual we’ll start by importing the necessary packages; for this tutorial
that includes nibabel to handle loading the MRI images (MNE-Python also
uses nibabel under the hood). We’ll also use a special Matplotlib function for adding outlines to text, so that text is
readable on top of an MRI image.
# Authors: The MNE-Python contributors.
# License: BSD-3-Clause
# Copyright the MNE-Python contributors.
import matplotlib.patheffects as path_effects
import matplotlib.pyplot as plt
import nibabel
import numpy as np
import mne
from mne.io.constants import FIFF
from mne.transforms import apply_trans
MRI coordinate frames#
Let’s start out by looking at the sample subject MRI. Following standard
FreeSurfer convention, we look at T1.mgz, which gets created from the
original MRI sample/mri/orig/001.mgz when you run the FreeSurfer
command recon-all.
Here we use nibabel to load the T1 image, and the resulting object’s
orthoview() method to view it.
data_path = mne.datasets.sample.data_path()
subjects_dir = data_path / "subjects"
subject = "sample"
t1_fname = subjects_dir / subject / "mri" / "T1.mgz"
t1 = nibabel.load(t1_fname)
t1.orthoview()
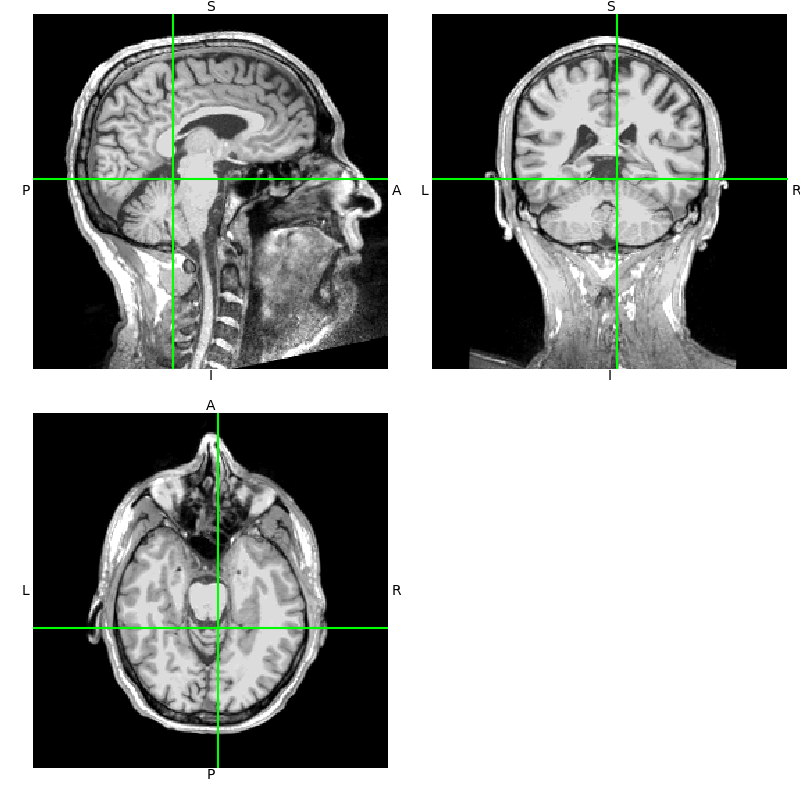
Notice that the axes in the
orthoview() figure are labeled
L-R, S-I, and P-A. These reflect the standard RAS (right-anterior-superior)
coordinate system that is widely used in MRI imaging. If you are unfamiliar
with RAS coordinates, see the excellent nibabel tutorial
Coordinate systems and affines.
Nibabel already takes care of some coordinate frame transformations under the hood, so let’s do it manually so we understand what is happening. First let’s get our data as a 3D array and note that it’s already a standard size:
data = np.asarray(t1.dataobj)
print(data.shape)
(256, 256, 256)
These data are voxel intensity values. Here they are unsigned integers in the
range 0-255, though in general they can be floating point values. A value
data[i, j, k] at a given index triplet (i, j, k) corresponds to some
real-world physical location (x, y, z) in space. To get its physical
location, first we have to choose what coordinate frame we’re going to use.
For example, we could choose a geographical coordinate
frame, with origin is at the center of the earth, Z axis through the north
pole, X axis through the prime meridian (zero degrees longitude), and Y axis
orthogonal to these forming a right-handed coordinate system. This would not
be a very useful choice for defining the physical locations of the voxels
during the MRI acquisition for analysis, but you could nonetheless figure out
the transformation that related the (i, j, k) to this coordinate frame.
Instead, each scanner defines a more practical, native coordinate system that
it uses during acquisition, usually related to the physical orientation of
the scanner itself and/or the subject within it. During acquisition the
relationship between the voxel indices (i, j, k) and the physical
location (x, y, z) in the scanner’s native coordinate frame is saved in
the image’s affine transformation.
We can use nibabel to examine this transformation, keeping in mind
that it processes everything in units of millimeters, unlike MNE where things
are always in SI units (meters).
This allows us to take an arbitrary voxel or slice of data and know where it
is in the scanner’s native physical space (x, y, z) (in mm) by applying
the affine transformation to the voxel coordinates.
[[-1.00000000e+00 1.15484021e-07 -1.91852465e-07 1.22726395e+02]
[ 8.56816911e-08 1.57160827e-08 1.00000000e+00 -1.18960930e+02]
[ 1.49011647e-08 -1.00000000e+00 6.40284092e-09 1.00712036e+02]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00 1.00000000e+00]]
Our voxel has real-world coordinates 0.726, -16.961, -18.288 (mm)
If you have a point (x, y, z) in scanner-native RAS space and you want
the corresponding voxel number, you can get it using the inverse of the
affine. This involves some rounding, so it’s possible to end up off by one
voxel if you’re not careful:
ras_coords_mm = np.array([1, -17, -18])
inv_affine = np.linalg.inv(t1.affine)
i_, j_, k_ = np.round(apply_trans(inv_affine, ras_coords_mm)).astype(int)
print(f"Our real-world coordinates correspond to voxel ({i_}, {j_}, {k_})")
Our real-world coordinates correspond to voxel (122, 119, 102)
Let’s write a short function to visualize where our voxel lies in an image, and annotate it in RAS space (rounded to the nearest millimeter):
def imshow_mri(data, img, vox, xyz, suptitle):
"""Show an MRI slice with a voxel annotated."""
i, j, k = vox
fig, ax = plt.subplots(1, figsize=(6, 6), layout="constrained")
codes = nibabel.orientations.aff2axcodes(img.affine)
# Figure out the title based on the code of this axis
ori_slice = dict(
P="Coronal", A="Coronal", I="Axial", S="Axial", L="Sagittal", R="Sagittal"
)
ori_names = dict(
P="posterior", A="anterior", I="inferior", S="superior", L="left", R="right"
)
title = ori_slice[codes[0]]
ax.imshow(data[i], vmin=10, vmax=120, cmap="gray", origin="lower")
ax.axvline(k, color="y")
ax.axhline(j, color="y")
for kind, coords in xyz.items():
annotation = "{}: {}, {}, {} mm".format(kind, *np.round(coords).astype(int))
text = ax.text(k, j, annotation, va="baseline", ha="right", color=(1, 1, 0.7))
text.set_path_effects(
[
path_effects.Stroke(linewidth=2, foreground="black"),
path_effects.Normal(),
]
)
# reorient view so that RAS is always rightward and upward
x_order = -1 if codes[2] in "LIP" else 1
y_order = -1 if codes[1] in "LIP" else 1
ax.set(
xlim=[0, data.shape[2] - 1][::x_order],
ylim=[0, data.shape[1] - 1][::y_order],
xlabel=f"k ({ori_names[codes[2]]}+)",
ylabel=f"j ({ori_names[codes[1]]}+)",
title=f"{title} view: i={i} ({ori_names[codes[0]]}+)",
)
fig.suptitle(suptitle)
return fig
imshow_mri(data, t1, vox, {"Scanner RAS": xyz_ras}, "MRI slice")
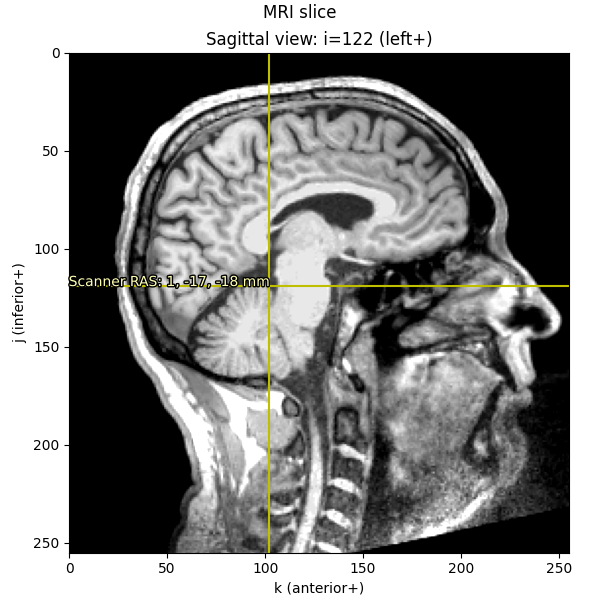
Notice that the axis scales (i, j, and k) are still in voxels
(ranging from 0-255); it’s only the annotation text that we’ve translated
into real-world RAS in millimeters.
“MRI coordinates” in MNE-Python: FreeSurfer surface RAS#
While nibabel uses scanner RAS (x, y, z) coordinates,
FreeSurfer uses a slightly different coordinate frame: MRI surface RAS.
The transform from voxels to the FreeSurfer MRI surface RAS coordinate frame
is known in the FreeSurfer documentation as Torig,
and in nibabel as vox2ras_tkr. This
transformation sets the center of its coordinate frame in the middle of the
conformed volume dimensions (N / 2.) with the axes oriented along the
axes of the volume itself. For more information, see
MEG/EEG and MRI coordinate systems.
Note
In general, you should assume that the MRI coordinate system for
a given subject is specific to that subject, i.e., it is not the
same coordinate MRI coordinate system that is used for any other
FreeSurfer subject. Even though during processing FreeSurfer will
align each subject’s MRI to fsaverage to do reconstruction,
all data (surfaces, MRIs, etc.) get stored in the coordinate frame
specific to that subject. This is why it’s important for group
analyses to transform data to a common coordinate frame for example
by surface or
volumetric morphing, or even by just
applying FreeSurfer’s MNI affine transformation to points.
Since MNE-Python uses FreeSurfer extensively for surface computations (e.g.,
white matter, inner/outer skull meshes), internally MNE-Python uses the
Freeurfer surface RAS coordinate system (not the nibabel scanner RAS
system) for as many computations as possible, such as all source space
and BEM mesh vertex definitions.
Whenever you see “MRI coordinates” or “MRI coords” in MNE-Python’s documentation, you should assume that we are talking about the “FreeSurfer MRI surface RAS” coordinate frame!
We can do similar computations as before to convert the given voxel indices into FreeSurfer MRI coordinates (i.e., what we call “MRI coordinates” or “surface RAS” everywhere else in MNE), just like we did above to convert voxel indices to scanner RAS:
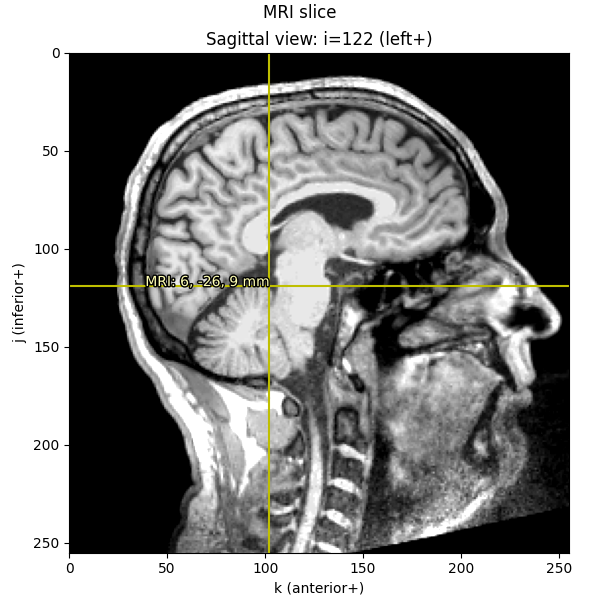
[[-1.00000000e+00 1.15484021e-07 -1.91852465e-07 1.22726395e+02]
[ 8.56816911e-08 1.57160827e-08 1.00000000e+00 -1.18960930e+02]
[ 1.49011647e-08 -1.00000000e+00 6.40284092e-09 1.00712036e+02]
[ 0.00000000e+00 0.00000000e+00 0.00000000e+00 1.00000000e+00]]
[[ -1. 0. 0. 128.]
[ 0. 0. 1. -128.]
[ 0. -1. 0. 128.]
[ 0. 0. 0. 1.]]
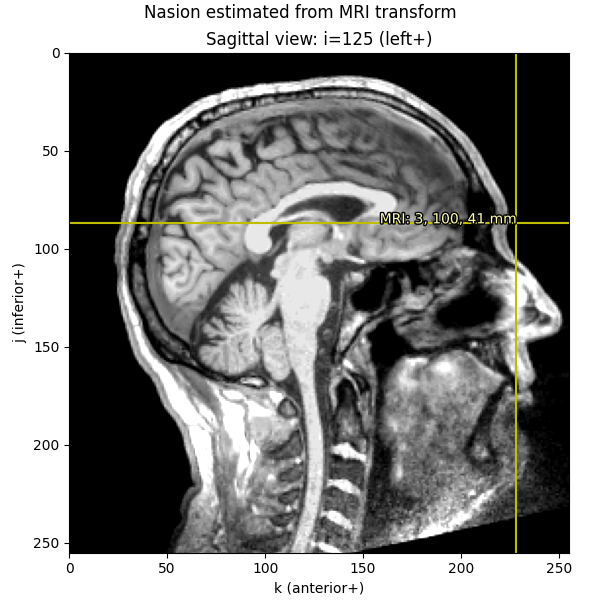
Knowing these relationships and being mindful about transformations, we can get from a point in any given space to any other space. Let’s start out by plotting the Nasion on a sagittal MRI slice:
fiducials = mne.coreg.get_mni_fiducials(subject, subjects_dir=subjects_dir)
nasion_mri = [d for d in fiducials if d["ident"] == FIFF.FIFFV_POINT_NASION][0]
print(nasion_mri) # note it's in Freesurfer MRI coords
<DigPoint | Nasion : (2.6, 99.8, 40.8) mm : MRI (surface RAS) frame>
When we print the nasion, it displays as a DigPoint and shows its
coordinates in millimeters, but beware that the underlying data is
actually stored in meters,
so before transforming and plotting we’ll convert to millimeters:
nasion_mri = nasion_mri["r"] * 1000 # meters → millimeters
nasion_vox = np.round(apply_trans(np.linalg.inv(Torig), nasion_mri)).astype(int)
imshow_mri(
data, t1, nasion_vox, dict(MRI=nasion_mri), "Nasion estimated from MRI transform"
)
We can also take the digitization point from the MEG data, which is in the “head” coordinate frame.
Let’s look at the nasion in the head coordinate frame:
info = mne.io.read_info(data_path / "MEG" / "sample" / "sample_audvis_raw.fif")
nasion_head = [
d
for d in info["dig"]
if d["kind"] == FIFF.FIFFV_POINT_CARDINAL and d["ident"] == FIFF.FIFFV_POINT_NASION
][0]
print(nasion_head) # note it's in "head" coordinates
Read a total of 3 projection items:
PCA-v1 (1 x 102) idle
PCA-v2 (1 x 102) idle
PCA-v3 (1 x 102) idle
<DigPoint | Nasion : (0.0, 102.6, 0.0) mm : head frame>
Notice that in “head” coordinate frame the nasion has values of 0 for the
x and z directions (which makes sense given that the nasion is used
to define the y axis in that system).
To convert from head coordinate frame to voxels, we first apply the head →
MRI (surface RAS) transform
from a trans file (typically created with the MNE-Python
coregistration GUI), then convert meters → millimeters, and finally apply the
inverse of Torig to get to voxels.
Under the hood, functions like mne.setup_source_space(),
mne.setup_volume_source_space(), and mne.compute_source_morph()
make extensive use of these coordinate frames.
trans = mne.read_trans(data_path / "MEG" / "sample" / "sample_audvis_raw-trans.fif")
# first we transform from head to MRI, and *then* convert to millimeters
nasion_dig_mri = apply_trans(trans, nasion_head["r"]) * 1000
# ...then we can use Torig to convert MRI to voxels:
nasion_dig_vox = np.round(apply_trans(np.linalg.inv(Torig), nasion_dig_mri)).astype(int)
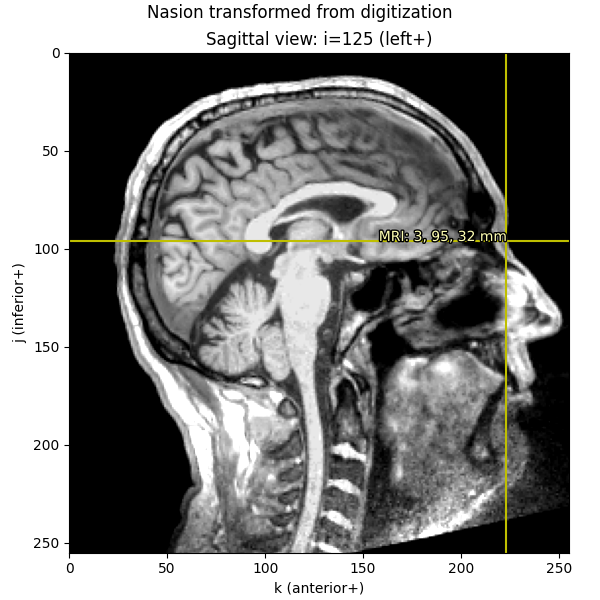
imshow_mri(
data,
t1,
nasion_dig_vox,
dict(MRI=nasion_dig_mri),
"Nasion transformed from digitization",
)
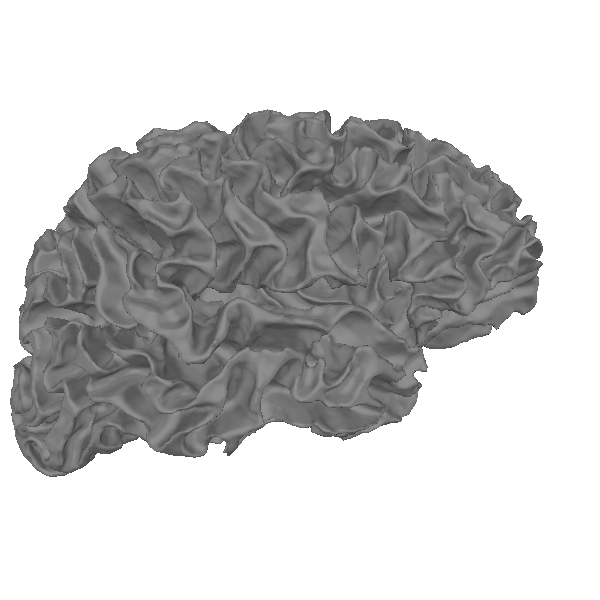
Using FreeSurfer’s surface reconstructions#
An important part of what FreeSurfer does is provide cortical surface
reconstructions. For example, let’s load and view the white surface
of the brain. This is a 3D mesh defined by a set of vertices (conventionally
called rr) with shape (n_vertices, 3) and a set of triangles
(tris) with shape (n_tris, 3) defining which vertices in rr form
each triangular facet of the mesh.
fname = subjects_dir / subject / "surf" / "rh.white"
rr_mm, tris = mne.read_surface(fname)
print(f"rr_mm.shape == {rr_mm.shape}")
print(f"tris.shape == {tris.shape}")
print(f"rr_mm.max() = {rr_mm.max()}") # just to show that we are in mm
rr_mm.shape == (156866, 3)
tris.shape == (313728, 3)
rr_mm.max() = 97.80481719970703
Let’s actually plot it:
renderer = mne.viz.backends.renderer.create_3d_figure(
size=(600, 600), bgcolor="w", scene=False
)
gray = (0.5, 0.5, 0.5)
renderer.mesh(*rr_mm.T, triangles=tris, color=gray)
view_kwargs = dict(elevation=90, azimuth=0) # camera at +X with +Z up
mne.viz.set_3d_view(
figure=renderer.figure, distance=350, focalpoint=(0.0, 0.0, 40.0), **view_kwargs
)
renderer.show()
We can also plot the mesh on top of an MRI slice. The mesh surfaces are
defined in millimeters in the MRI (FreeSurfer surface RAS) coordinate frame,
so we can convert them to voxels by applying the inverse of the Torig
transform:
rr_vox = apply_trans(np.linalg.inv(Torig), rr_mm)
fig = imshow_mri(data, t1, vox, {"Scanner RAS": xyz_ras}, "MRI slice")
# Based on how imshow_mri works, the "X" here is the last dim of the MRI vol,
# the "Y" is the middle dim, and the "Z" is the first dim, so now that our
# points are in the correct coordinate frame, we need to ask matplotlib to
# do a tricontour slice like:
fig.axes[0].tricontour(
rr_vox[:, 2],
rr_vox[:, 1],
tris,
rr_vox[:, 0],
levels=[vox[0]],
colors="r",
linewidths=1.0,
zorder=1,
)
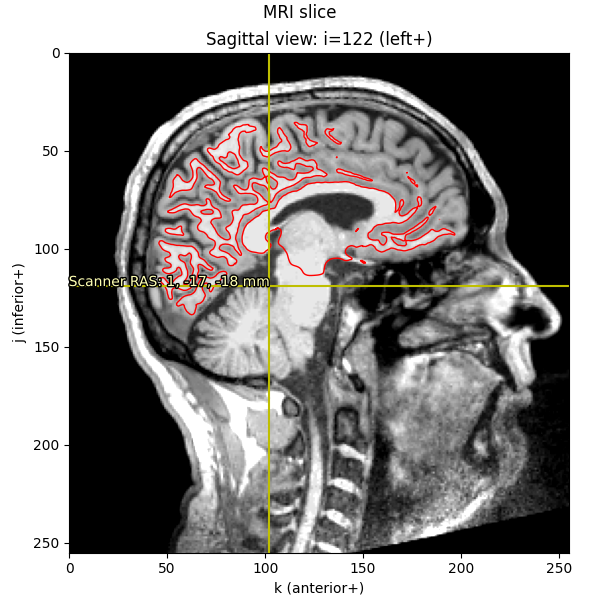
This is the method used by mne.viz.plot_bem() to show the BEM surfaces.
Cortical alignment (spherical)#
A critical function provided by FreeSurfer is spherical surface alignment of cortical surfaces, maximizing sulcal-gyral alignment. FreeSurfer first expands the cortical surface to a sphere, then aligns it optimally with fsaverage. Because the vertex ordering is preserved when expanding to a sphere, a given vertex in the source (sample) mesh can be mapped easily to the same location in the destination (fsaverage) mesh, and vice-versa.
renderer_kwargs = dict(bgcolor="w")
renderer = mne.viz.backends.renderer.create_3d_figure(
size=(800, 400), scene=False, **renderer_kwargs
)
curvs = [
(
mne.surface.read_curvature(
subjects_dir / subj / "surf" / "rh.curv", binary=False
)
> 0
).astype(float)
for subj in ("sample", "fsaverage")
for _ in range(2)
]
fnames = [
subjects_dir / subj / "surf" / surf
for subj in ("sample", "fsaverage")
for surf in ("rh.white", "rh.sphere")
]
y_shifts = [-450, -150, 450, 150]
z_shifts = [-40, 0, -30, 0]
for name, y_shift, z_shift, curv in zip(fnames, y_shifts, z_shifts, curvs):
this_rr, this_tri = mne.read_surface(name)
this_rr += [0, y_shift, z_shift]
renderer.mesh(
*this_rr.T,
triangles=this_tri,
color=None,
scalars=curv,
colormap="copper_r",
vmin=-0.2,
vmax=1.2,
)
zero = [0.0, 0.0, 0.0]
width = 50.0
y = np.sort(y_shifts)
y = (y[1:] + y[:-1]) / 2.0 - width / 2.0
renderer.quiver3d(zero, y, zero, zero, [1] * 3, zero, "k", width, "arrow")
view_kwargs["focalpoint"] = (0.0, 0.0, 0.0)
mne.viz.set_3d_view(figure=renderer.figure, distance=1050, **view_kwargs)
renderer.show()

Let’s look a bit more closely at the spherical alignment by overlaying the two spherical meshes as wireframes and zooming way in (the vertices of the black mesh are separated by about 1 mm):
cyan = "#66CCEE"
black = "k"
renderer = mne.viz.backends.renderer.create_3d_figure(
size=(800, 800), scene=False, **renderer_kwargs
)
surfs = [
mne.read_surface(subjects_dir / subj / "surf" / "rh.sphere")
for subj in ("fsaverage", "sample")
]
colors = [black, cyan]
line_widths = [2, 3]
for surf, color, line_width in zip(surfs, colors, line_widths):
this_rr, this_tri = surf
# cull to the subset of tris with all positive X (toward camera)
this_tri = this_tri[(this_rr[this_tri, 0] > 0).all(axis=1)]
renderer.mesh(
*this_rr.T,
triangles=this_tri,
color=color,
representation="wireframe",
line_width=line_width,
render_lines_as_tubes=True,
)
mne.viz.set_3d_view(figure=renderer.figure, distance=150, **view_kwargs)
renderer.show()

You can see that the fsaverage (black) mesh is uniformly spaced, and the mesh for subject “sample” (in cyan) has been deformed along the spherical surface by FreeSurfer. This deformation is designed to optimize the sulcal-gyral alignment.
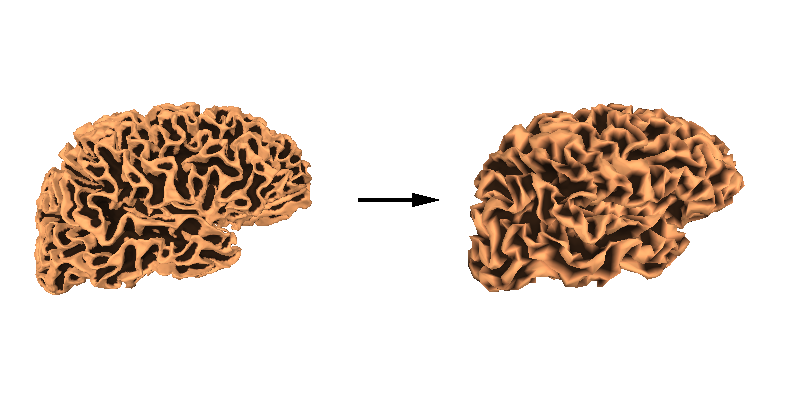
Surface decimation#
These surfaces have a lot of vertices, and in general we only need to use a subset of these vertices for creating source spaces. A uniform sampling can easily be achieved by subsampling in the spherical space. To do this, we use a recursively subdivided icosahedron or octahedron. For example, let’s load a standard oct-6 source space, and at the same zoom level as before visualize how it subsampled (in red) the dense mesh:
src = mne.read_source_spaces(subjects_dir / "sample" / "bem" / "sample-oct-6-src.fif")
print(src)
red = "#EE6677"
renderer = mne.viz.backends.renderer.create_3d_figure(
size=(800, 800), scene=False, **renderer_kwargs
)
rr_sph, _ = mne.read_surface(fnames[1])
for tris, color in [(src[1]["tris"], cyan), (src[1]["use_tris"], red)]:
# cull to the subset of tris with all positive X (toward camera)
tris = tris[(rr_sph[tris, 0] > 0).all(axis=1)]
renderer.mesh(
*rr_sph.T,
triangles=tris,
color=color,
representation="wireframe",
line_width=3,
render_lines_as_tubes=True,
)
mne.viz.set_3d_view(figure=renderer.figure, distance=150, **view_kwargs)
renderer.show()

Reading a source space...
Computing patch statistics...
Patch information added...
Distance information added...
[done]
Reading a source space...
Computing patch statistics...
Patch information added...
Distance information added...
[done]
2 source spaces read
<SourceSpaces: [<surface (lh), n_vertices=155407, n_used=4098>, <surface (rh), n_vertices=156866, n_used=4098>] MRI (surface RAS) coords, subject 'sample', ~27.5 MiB>
We can also then look at how these two meshes compare by plotting the original, high-density mesh as well as our decimated mesh white surfaces.
renderer = mne.viz.backends.renderer.create_3d_figure(
size=(800, 400), scene=False, **renderer_kwargs
)
y_shifts = [-125, 125]
tris = [src[1]["tris"], src[1]["use_tris"]]
for y_shift, tris in zip(y_shifts, tris):
this_rr = src[1]["rr"] * 1000.0 + [0, y_shift, -40]
renderer.mesh(
*this_rr.T,
triangles=tris,
color=None,
scalars=curvs[0],
colormap="copper_r",
vmin=-0.2,
vmax=1.2,
)
renderer.quiver3d([0], [-width / 2.0], [0], [0], [1], [0], "k", width, "arrow")
mne.viz.set_3d_view(figure=renderer.figure, distance=450, **view_kwargs)
renderer.show()
Warning
Some source space vertices can be removed during forward computation. See Head model and forward computation for more information.
FreeSurfer’s MNI affine transformation#
In addition to surface-based approaches, FreeSurfer also provides a simple
affine coregistration of each subject’s data to the fsaverage subject.
Let’s pick a point for sample and plot it on the brain:
brain = mne.viz.Brain(
"sample", "lh", "white", subjects_dir=subjects_dir, background="w"
)
xyz = np.array([[-55, -10, 35]])
brain.add_foci(xyz, hemi="lh", color="k")
brain.show_view("lat")
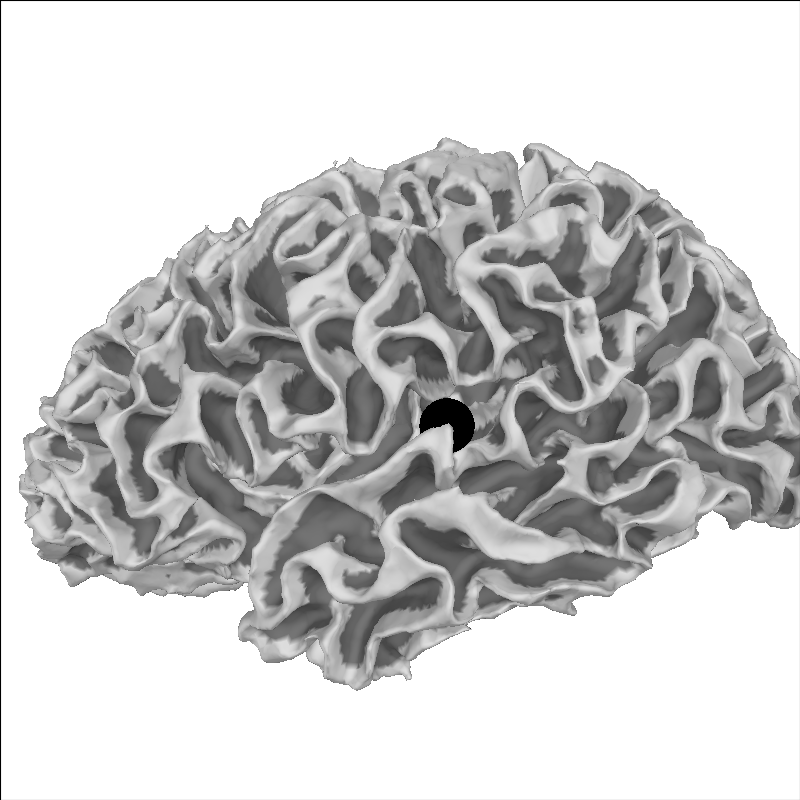
We can take this point and transform it to MNI space:
mri_mni_trans = mne.read_talxfm(subject, subjects_dir)
print(mri_mni_trans)
xyz_mni = apply_trans(mri_mni_trans, xyz / 1000.0) * 1000.0
print(np.round(xyz_mni, 1))
<Transform | MRI (surface RAS)->MNI Talairach>
[[ 1.02248488 -0.00844919 -0.03621711 0.00111715]
[ 0.07107091 0.91486582 0.40609791 -0.02300193]
[ 0.00875602 -0.43369992 1.02811882 -0.03356932]
[ 0. 0. 0. 1. ]]
[[-56.3 -21.8 6.3]]
And because fsaverage is special in that it’s already in MNI space
(its MRI-to-MNI transform is identity), it should land in the equivalent
anatomical location:
brain = mne.viz.Brain(
"fsaverage", "lh", "white", subjects_dir=subjects_dir, background="w"
)
brain.add_foci(xyz_mni, hemi="lh", color="k")
brain.show_view("lat")
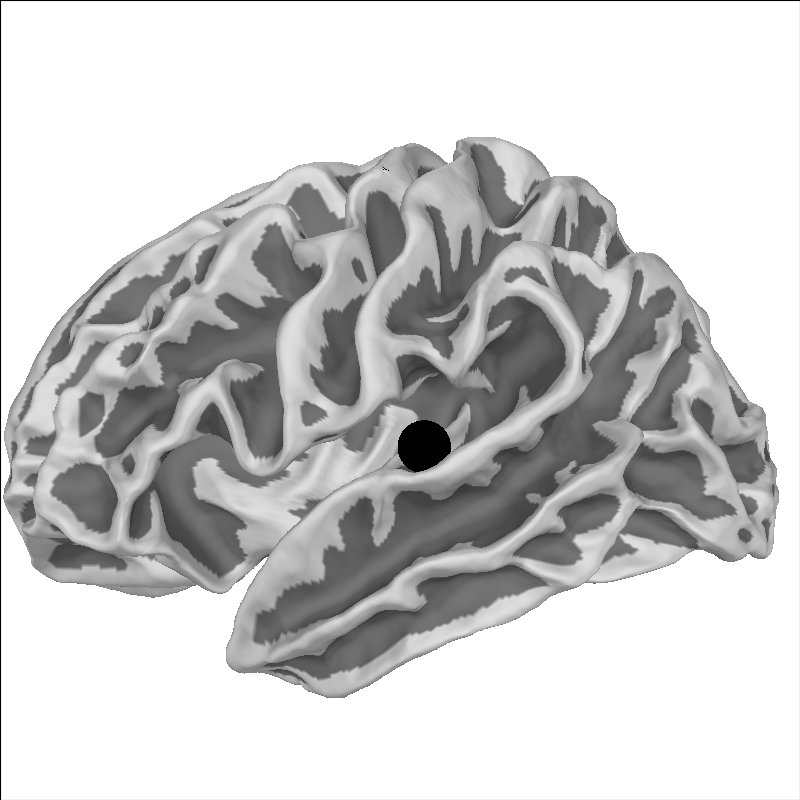
Understanding the inflated brain#
It takes a minute to interpret data displayed on an inflated brain. This visualization is very helpful in showing more of a brain in one image since it is difficult to visualize inside the sulci. Below is a video relating the pial surface to an inflated surface. If you’re interested in how this was created, here is the gist used to create the video: https://gist.github.com/alexrockhill/b5a1ce6c6ba363cf3f277cd321a763bf.
Total running time of the script: (0 minutes 13.659 seconds)